How to solve Syllogism: Logical Reasoning
- 17/04/2024
- Posted by: Yashita
- Category: CAT Preparation

Flavius: “Have you forgot me, sir?”
Timon: “Why dost ask that? I have forgot all men;
Then, if thou grant’st thou’rt a man, I have forgot thee.”
A witty syllogism from Timon to Flavius to tell that he must have forgotten him like he has forgotten all other men. It can be expanded in a three-set argument as: “I usually do forget, as I have forgotten everyone. Therefore, I have forgotten you as well.” The given lines are from a play by William Shakespeare
So, is it cloudy for you to understand Syllogism and crack them?
Syllogism is an important part of the CAT logical reasoning section and carries significant importance within this section. Typically, around 3-4 questions related to syllogism are included in the CAT exam each year. As a result, it is crucial to thoroughly prepare for this topic and practice a diverse range of syllogism questions to perform well on the exam.
To solve the questions based on Syllogism in CAT 2024, candidates first have to understand the meaning of statements then move to the conclusions and after that mark the answer. With the help of some methods like Venn Diagrams and analytical methods, syllogism questions can be solved easily.
“What is Syllogism?”
You’ve probably heard of logic. Well, syllogism is a type of logical argument using deductive reasoning. While syllogism is a weird word, it’s quite simple to understand. Syllogism derives from the Greek word syllogismos, meaning conclusion or inference. In simple words syllogism is a form of deductive reasoning where you arrive at a specific conclusion by examining premises or ideas.
For example:
All roses are flowers.
This is a rose.
I’m holding a flower.
Many syllogisms contain three components.
- Major premise – All roses are flowers.
- Minor premise – This is a rose.
- Conclusion – I’m holding a flower.
Syllogism Fallacy
Syllogism may also be used to form incorrect conclusions that are odd. For instance, “All crows are black, and the bird in my cage is black. So, the bird in my cage is a crow.” This is a false argument, as it implies a conclusion that “all blackbirds are crows,” which is incorrect. It is known as “syllogism fa.” Another example of syllogism fallacy is “Some televisions are black and white, and all penguins are black and white. Therefore, some televisions are penguins.” You can easily see that the conclusion is practically impossible, and in fact has a comical outcome.
Syllogism for CAT Logical Reasoning Formulas
Some rules to solve the problem of Syllogism for CAT Logical Reasoning are as follows.
- All+All=All
- All+No=No
- All+Some=No conclusion
- Some+All=Some
- Some+No= Some Not
- Some+Some= No Conclusion
- No+All = Some Not(Reversed)
- No+Some=Some Not (Reversed)
- No+No=No Conclusion
Syllogism for CAT Logical Reasoning Shortcut Tricks
Some steps to convert a solution into the possibility are given below:
- If All A are B, then we can say – Some B are not A is a Possibility.
- If Some B are not A, then we can say – All A are B is a possibility.
- If Some A are B, then we can say – All A are B is a Possibility and All B are A is a Possibility.
- All Some <———> Not Reversed
- Some <———-> All
- NO Conclusion = Any Possibility is true
CAT Syllogism: Basic Concepts
- Syllogisms consist of statements and conclusions.
- Candidates will be given a set of statements and candidates have to find the correct conclusion from the assumed propositions. .
- Syllogisms tests the candidates deductive reasoning skills.
- This topic is important as it is an indicator of a candidate’s real world performance in a business setting where they have to deal with such scenarios often.
- It is important to remember that a syllogism contains all the information required to reach the accurate conclusion.
- Under new circumstances shall candidates assume that they require more information.
- Definite Conclusions: Definite conclusions are always true based on the statements give.
- Possibilities: They can be true but not accurate.
How to Solve CAT Syllogisms Questions?
- There are primarily 2 ways to solve syllogisms, i.e through venn diagrams and through analytical method.
- The Venn Diagram method is in use more frequently as it is easier and faster as well.
- In Venn Diagrams, a diagram contains the information available to candidates can find out the answer through the diagram.
- The Analytical Method for solving syllogisms is requires mental sharpness.
- Candidates who are exceptional at reasoning can solve syllogism mentally by visually picturing the information available to them.
Syllogism : Venn Diagram
- A Venn diagram is a figure that represents or visually portrays the relationship between the objects as given in the statements provided.
- Usually, it is in the form of circles and lines/flowcharts.
- Each term can be represented as a circle. For eg, if there are three classes there will be three circles.
- In the figure given below, the area in the circle represents the members of the class.
- The area outside the circles represents all others.
- Shading represents that no individual exists in that specific area.
- Empty spaces mean that there is no information about it.
Solved Examples of Syllogism for CAT
For Example 1:Which of the two conclusions can be concluded on the basis of given statements?
- Statements:
- Some parrots are scissors.
- Some scissors are not combs.
- Conclusions:
- Some scissors are parrots.
- Some combs are parrots.
Solution: Now, in this case, the possible conclusion is: Some scissors are parrots (I to I), as the universal principal no. 4 says, that with two particular statements only I to I is possible. Therefore, only 1 conclusion is possible. Nothing else is possible.
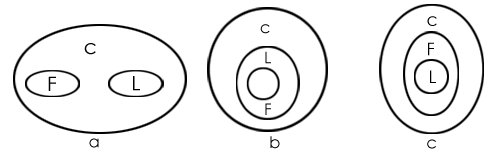
For Example 2 : Which of the two conclusions can be concluded on the basis of given statements?
- Statements:
- All flowers are candles.
- All lanterns are candles.
- Conclusions:
- Some flowers are lanterns.
- Some candles are lanterns.
Solution: Three possible diagrams is show in the above for the given statements.
Conclusion I follows from last two possible solutions, but does not follow from the first possible solution. Therefore, this conclusion is false.
Conclusion II follows from all the three possible solutions.
Therefore, conclusion II is true.
For Example 3: Which of the two conclusions can be concluded on the basis of given statements?
- Statements:
- All prisoners are men.
- No man is educated.
- Conclusions:
- All prisoners are uneducated.
- Some men are prisoners.
Solution: So their are two possible diagrams is show in below for the given statements.


