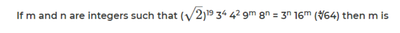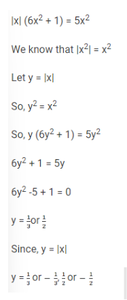29/01/2024 3:00 pm
Algebra
64
Posts
11
Users
107
Reactions
3,681
Views
5
Q1. The number of the real roots of the equation 2cos(x(x + 1)) = 2x + 2-x is
4
25/12/2023 5:57 pm
The number of integers n that satisfy the inequalities |n - 60| < |n - 100| < |n - 20| is
-
21
-
18
-
20
-
19
Madhav 26/12/2023 11:14 am
Answer :-
|n - 60| < |n - 100| < |n - 20|
To solve this question, we need to know the basic concept that ‘if x and y are two points on the number line, then the distance between these two points can be represented by |x - y| or |y - x|.’
Let's take the first part of the inequality
|n - 60| < |n - 100|
This inequality holds good for the values of n below 80. So this is the turning point.
Hence ‘n’ should be less than 80.
Now Let's check for the later part of the inequality.
|n - 100| < |n - 20|
This inequality holds good for the values of n above 60. So, 60 is the turning point here.
Hence ‘n’ should be greater than 60.
Therefore, the values of ‘n’ range from 61 to 79.
So, the total possible integers that satisfy this inequality are 19.
4
05/01/2024 12:28 pm
If log2[3 + log3{4 + log4(x - 1)}] - 2 = 0 then 4x equals
Shivangi Garg 05/01/2024 12:51 pm
Sir, Yeh thik hai?
log2[3+log3{4+log4(x-1)}]- 2= 0
log2[3 + log3{4 + log4(x - 1)}] = 2
3 + log3{4 + log4(x - 1)} = 4 ( ∵ logaN = x ⇒ N = ax )
log3{4 + log4(x - 1)} = 1
4 + log4(x - 1) = 3
log4(x - 1) = -1
x - 1 = 1/4
4x = 5
4
07/02/2024 12:08 pm
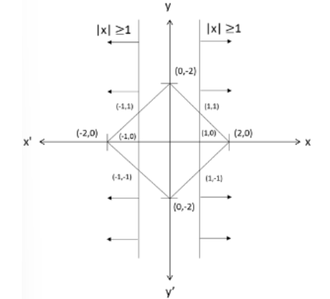
Q1. Let S be the set of all points (x,y) in the x-y plane such that
|x| + |y| ≤ 2 and |x| ≥ 1. Then, the area, in square units, of the region represented by S equals ?
Shivangi Garg 08/02/2024 12:11 pm
This post was modified 11 months ago by Shivangi Garg
Since we have cancelled y in our first step, x = 0 is also a solution
So, Number of possible solutions = 4 + 1 = 5
4
07/02/2024 12:47 pm
Shivangi Garg 08/02/2024 12:26 pm
@neraj-naiyar Sir,
For x = -2,
x2 - x - 6 = x +2
4 + 2 - 6 = x + 2
0 - 2 = x
-2 = x. Therefore, x = - 2 works
Similarly, Solving -(x2 - x - 6) = x + 2
-x2 + x + 6 = x + 2
x2 = 4
x = +2 or -2
For the solution to be valid, x2 - x - 6 must be negative
When x = +2,
-x2 + x + 6 = x +2
-4 + 2 + 6 = x + 2
+ 2 = x Therefore, x = 2 works.
Therefore, Product of distinct roots = 2 x -2 x 4 = -16
2
09/02/2024 3:06 pm
Q1. A is the average of 10 given numbers. B is the average after 2 of the numbers were replaced by 3 other different numbers. The average of the removed nu0mbers is 48 and the average of the newly included numbers is 56. If A + B = 438, then the value of A - B is:
(a) 21
(b) 14
(c) 12
(d) 26
This post was modified 11 months ago by Ujjwal Dwivedi
Sachin Yadav 10/02/2024 4:04 pm
Sol.2 (b)
Total sum of 10 number = 10A
According to the question,
⇒ (-48 × 2) + (3 × 56) + (sum of rest of number) = 11B
Then, 11B - 10A = 72 ... (i)
Given that, A + B = 438 ..... (ii)
Solving on Eq (i) and Eq(ii) we get,
B = 212 and A 226.
So, A - B = 14
2
20/02/2024 3:35 pm
Q1. What is the square of root of 99999 ?
A) 316.23
B) 316.22
C) 316.21
D) 316.20
1
01/11/2020 11:36 pm
Topic starter
In the expansion of (a + b + c)20, find
A.Number of terms?
B. Sum of the coefficients
1
21/02/2024 12:25 pm
Q.4 What is cube root of 55555:-
A) 38.17
B) 38.16
C) 38.15
D) 38.14
0
01/11/2020 11:36 pm
Topic starter
If a + b + c = 6, find the maximum value of a3b2c, where all a, b and c are positive real
numbers.
Anonymous 12/01/2022 10:32 am
As i checked all the conversions are very informative , Thank you for your solutions.
0
01/11/2020 11:37 pm
Topic starter
Both x2 + 16x – q = 0 and x2 – 11qx + 25 = 0 have real roots. The number of positive integral values of q is _____ .
A. 39 B.70 C. 60 D. 64
0
01/11/2020 11:39 pm
Topic starter
The equation 5x + 7y = k has 7 solutions in which both x, y are non-negative integers. What is the minimum value of k?
A. 210 B. 280 C. 223 D. 290
0
01/11/2020 11:40 pm
Topic starter
The sum of the first eight terms of a geometric progression is 510 and the sum of the first four terms of the geometric progression is 30. Find the first term of the geometric progression, given that it is positive.