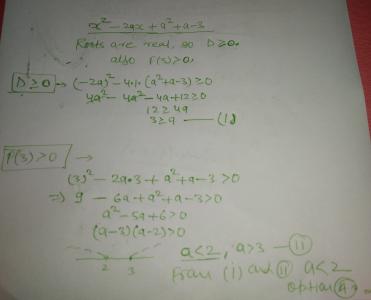19/02/2018 6:16 pm
Topic starter
Algebra
74
Posts
24
Users
1
Reactions
35 K
Views
0
let the quadratic eq ax^2 +bx + c be such that a,b,c are distinct and each of a,b,c belong to {1,2,3.....n} such that x+1 divides ax^2+ bx +c.If such quad.polynomials are < 99,then max(n)=?
a)14 b)15 c)16 d)18 e)none of these
Aditya Dang 22/06/2021 8:03 am
This post was modified 4 years ago 2 times by Aditya Dang
Since, x+1 satisfies the equation ax^2+ bx+ c=0. Therefore, a(-1)^2+b(-1)+c=0. So, a - b+ c=0.
Now, a + c=b. Minimum value of b is 3. Number of quadratic equations will exceed 99 when b=12. So, the answer is none of these.
40 questions & discussions are there under this sub-topic
0
20/02/2018 12:04 pm
The number of non-negative integer solutions of a + b = c ---> c – 1C1 = c - 1. Therefore, number of solutions when c = 2, 3, 4, .., 15 = 1, 2, 3, 4, ... 14 = 105. Out of these we have to remove solutions where a and b are not distinct. it happens when c is even. The number of cases = 7. Therefore, total solutions = 105 - 7 = 98 and answer is b.
if y is an integer such that y>=4 and x=y*y -2y,then largest number that divides x*x-8x=?
If you substitute x=y2-2y into x2-8x you will obtain,
x2-8x = (y-4)(y-2)(y)(y+2)
If y is odd:
then x2-8x is divisible by 3
If y is even:
then it has to be divisible by 2 (4!) = 48
0
31/03/2018 2:44 pm
For the equation 4x2 - 2xy - 8x + y + 9 = 0, find the number of positive integral solutions.
0
31/03/2018 2:44 pm
Hi Tina,
Plese find the solution
We want to find number of positive integral solutions for (x,y) 4x2 - 2xy - 8x + y + 9 = 0
=>4x2 - 8x + 9 = (2x - 1)y
=>y = (4x2 - 8x + 9)/(2x - 1) = (2x -3) + 6/(2x-1).
Only two values satisfy. (1,5), (2,3)
0
31/03/2018 2:47 pm
Hello Kinshuk !
a^19 + 17a - 19 = 0
a^19 = 19 -17a
similarly , b^19 = 19 - 17b ,
c^19 = 19 - 17c .....
So a^19 + b^19 + c^19 +....... = 19 - 17a + 19 - 17b + 19 - 17c +......
= 19 × 19 - 17 ( a+ b + c +....)
Sum of roots => 0
19 × 19 - 17 × 0 = 361.
0
10/07/2018 7:03 pm
Hi Gaurav ! PFA the Solution
0
26/07/2018 5:19 pm
The number of quadratic equation with leading coefficient 1 which are unchanged by squaring their roots is?
Hello Yamin ,
a and b are roots
So , a + b = a² + b²
and ab = a²b²
=> ab(ab - 1)
i) a = 0
=> b = 0 or 1
ii) b = 0
=> a = 0 or 1
iii) ab = 1
a + 1/a = a² + 1/a²
=> a⁴ - a³- a + 1 = 0
=> (a³ - 1)(a - 1) = 0
=> a = 1 or w or w²
=> b = 1 or w² or w
So, equation are x² = 0
x² - x= 0
x² - 2x + 1 = 0 and x² + x + 1 = 0
4 such equations.
0
26/07/2018 5:22 pm
If the roots of x^2 - 2ax + a^2 + a -3 are real and less than 3 then
A. a is less than two
B. a lies between 2 and 3
C. a is greater than 4
TG Team 26/07/2018 6:12 pm
Hello Yamin,
put x = 0 in the expression x² - 2ax + a² + a - 3
it reduces to
a² + a - 3 = 0
a = -1/2 + (√13)/2 and -1/2 + √13/2
Here roots are less than 2 hence option (B) and (C) got eliminated.
Hence , Option (A ) is the correct answer .
Anonymous 26/10/2021 6:14 pm
This was very difficult question, It took an hour to solve me this question.
0
26/07/2018 5:25 pm
If eq x^3 - ax^2 + bx - a =0 has 3 real roots the what is true?
A. a=1
B. b=1
C. b not equal to 1
TG Team 26/07/2018 5:59 pm
x³ - ax² + bx -a = 0
x² ( x - a) + b ( x-a) = 0
if , b = 1 , then the equation reduces to
x²( x - a) + (x-a) = 0
(x-a)(x² + 1) = 0
it has one real root a and two imaginary roots . hence b ≠ 1 .
Option C.
0
26/07/2018 5:26 pm
3x^2 + px + 3 has p greater tha 0. One root is square of other. Then what is the value of p?
TG Team 26/07/2018 5:51 pm
Hello Yamin,
Sum of roots = a + a² = -p/3 ..... (1)
Product of the roots = a³ = 3/3 = 1 ... (2)
a³ -1 = 0
(a-1)( a² + a + 1 ) = 0
(a-1) = 0 or ( a² + a + 1 ) = 0
a² + a = - 1
From equation (1)
-1 = -p/3
p = 3 🙂
0
26/07/2018 5:29 pm
In what positive base b does 4×12=103 hold?
0
26/07/2018 5:31 pm
Find the condition for the equation ax^2 + bx + c = 0 for one root is n times the other
0
31/07/2018 10:24 am
X=2+2^2/3+2^1/3, then the value of x^3-6x^2+6x?
Hello Tarishi
(x - 2) = 2⅔ + 2⅓
Cubing both sides
(x - 2)³ =( 2⅔ + 2⅓ )³
= (2⅔)³ + ( 2⅓)³ + 3•2⅔• 2⅓( 2⅔ + 2⅓ )
[( a + b)³ = a³ + b³ + 3ab ( a + b )]
6 + 3 × 2(2⅔ + 2⅓) = 6 + 6(x - 2)
x³ - 8 - 6x² + 12x = 6 + 6x - 12
x³ - 6x² + 6x = 6 - 12 + 8 = 2.
0
31/07/2018 10:28 am
Solve the equation:x^4-2x^3+4x^2+6x-21=0 if two of its roots are equal in magnitude but opposite in sign .
0
31/07/2018 2:35 pm
If the constant term of (2x-1/x)^n is -160 ! Find n
TG Team 31/07/2018 3:17 pm
Hello Tarishi ,
General term of (2x – 1/x) n = nCr (2x)r (-1/x)(n-r)
= nCr (2r) (-1)(n-r) xr(1/x)(n-r)
Now ,
for constant term , power of x = 0
r = n – r
n = 2r
Constant Term = 2rCr2r (-1)r= - 160
r = 3 satisfies , Hence n = 2r = 6 .
Page 1 / 3
Next