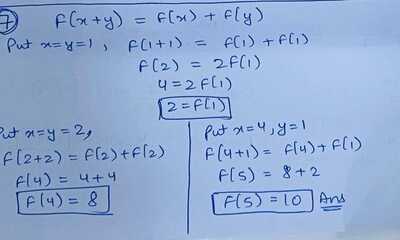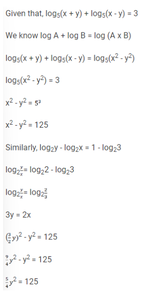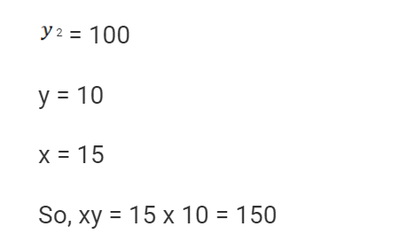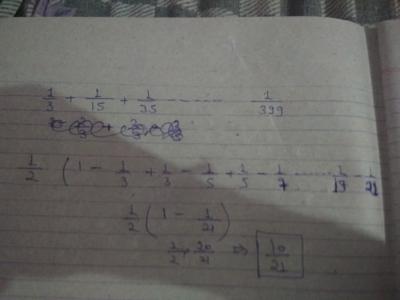20/02/2018 5:53 pm
Topic starter
Algebra
297
Posts
26
Users
18
Reactions
56.9 K
Views
0
118 questions & discussions are there under this sub-topic
3
06/01/2024 2:11 pm
A real valued function f(x), f(y) is such that f(x+y)=f(x)+f(y) for all real values of x and y. Find the value of f(5), if f(2)=4.
3
17/01/2024 4:16 pm
Q.1 The mean of all 4 digit even natural numbers of the form 'aabb', where a>0, is
- 5544
- 4466
- 4864
- 5050
This post was modified 11 months ago by Madhav
Neraj (TG) 19/01/2024 12:15 pm
Even numbers so b = 0
1100 1122 1144 1166 1188
2200 2222 2244 … … 9900 … … … …
By adding
5(1100+...+9900) +9(22+44+66+88)/45 {Since the term is common 5 times and 9 times}
(5×100×11×45) +9×22(1+2+3+4)/45
= 5544
3
30/01/2024 3:37 pm
Q1. The number of the real roots of the equation 2cos(x(x + 1)) = 2x + 2-x is
1
09/09/2018 4:08 am
If f(x) = (x-1)/(x-2), what is f invesrse (4) ?
TG Team 09/09/2018 11:42 am
f(x) = ( x - 1)/( x - 2)
y =( x - 1 )/(x -2)
yx - 2y = x - 1
yx - x = 2y - 1
x ( y-1) = 2y -1
x = (2y -1)/( y-1)
f-1(x) = (2x -1 )/( x -1)
f-1(4) = (8 -1)/( 4-1)= 7/3
1
24/09/2018 1:49 pm
Hello sir , this is a doubt from copycat 05 , please explain the solution of this problem -
Find the sum of the given infinite series : 3 + 5/(1+22 ) + 7/(1+22+32) +..............
aniket prajapati 24/09/2018 7:45 pm
In miscellaneous type of series find nth term and than try to solve ..
1
02/10/2018 12:36 pm
TG Team 02/10/2018 2:28 pm
Highest possible marks : 60
Lowest possible marks : -20
So a total off 80 x 3+1=241 possible scores but scores such as 59+2/3, 59 + 1/3 and 58 + 1/3 are not possible to get Hence , 241 - 3 = 238 possibilities.
1
10/10/2018 9:47 pm
Q-20
aniket prajapati 12/10/2018 12:45 am
when we cube root any no. then values can be approximated but when we square or cube any no. then value increases rapidly and we get increased value than the approximated one
here main part is squaring 3.1 which will give 9.61 and rest u can approximate
=(9 + 125 -9 +25*10 -125)^1/3 *9.61*10
=5*9.6*10
=480 option (5)
1
20/10/2018 3:52 pm
Find the last three digits of 79999
TG Team 20/10/2018 6:09 pm
The quicker way to calculate last three digits of a number is to calculate the remainder by 1000.
1000 = 125 x 8
79999/8 = (-1)9999 = -1 or 7.
79999/125
Phi(125) = 100
7100k gives a remainder of 1 when divided by 125 .
so 710000 gives the remainder 1.
Lets say 79999 gives remainder R when divided by 125.
So , 79999 x 7 /125 => 1
7R/125 => 1
R = 18.
Using Chinese Remainder Theorem:
125a + 18 = 8b + 7 gives 143.
1
01/11/2018 10:34 am
TG Team 01/11/2018 12:27 pm
To win the game A has to leave exactly one coin on the table so that B has to pick it up and would lose the game .
So A make his strategy to remove 9 coins from the table
So , 9 - 4 - 4 i.e 1 coin.
rachit 01/11/2018 12:41 pm
if u leave pick matchstick there is chance that other player will get chance to leave one coin for u. .. yes i don't know the ans but 1 can't be the ans this is certainly true
1
08/10/2019 8:18 pm
the maximum possible value of y = min(1/2 - 3x^2/4 , 5x^2/4) for the range 0<x<1 is ? (cat 1993)
a. 1/3
b. 1/2
c. 5/27
d. 5/ 16
1
03/02/2024 2:27 pm
Q1. Let x and y be positive real numbers such that log5(x + y) + log5(x - y) = 3, and log2y - log2x = 1 - log23. Then xy equals ?
0
22/02/2018 12:22 pm
Hello Tina,
Please find the solution,
r + (1/r) = 2007 + (1/2007) and
s + (1/s) = 2006 + (1/2006)
=> r = 2007 or (1/2007) and
s = 2006 or (1/2006)
We can verify these results by solving the two quadratic equations also
2007r2 - (20072 + 1)r + 2007 = 0 and
2006s2 - (20062 + 1)s + 2006 = 0
Now (r - s) is maximum when r is maximum and s is smallest.
So (r - s)maximum = rmax - smin = 2007 - (1/2006) = (4026041/2006) = 2006.9999
0
16/03/2018 5:32 pm
Topic starter
Hello, sir please solve this questions.
If x + 1 = x2 and x > 0, then 2x4 is:
abhi07 16/03/2018 5:44 pm
Hi Tina,
x + 1 = x2
x2 – x – 1 =0
x=(1+sqrt(1+4))/2
x = (1+sqrt5)/2
x2 =(6 + 2sqrt5)/4
x2 =(3+sqrt5)/2
x4 =(14+6sqrt5)/4
x4 =(7+3sqrt5)/2
2x4 =7+ 3sqrt5
Page 1 / 8
Next