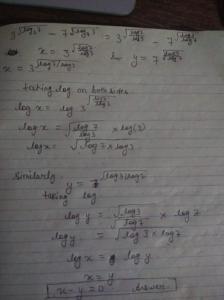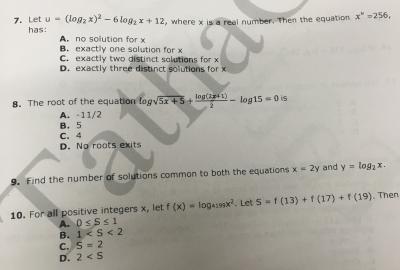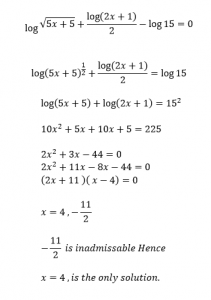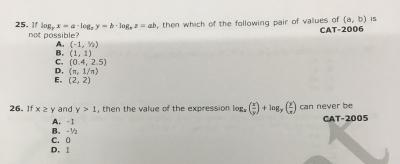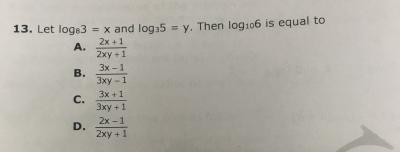28/08/2018 8:38 pm
Notifications
Clear all
Algebra
297
Posts
26
Users
18
Reactions
69.3 K
Views
0
31/08/2018 11:43 pm
This question is my doubt from copy cat 03-
A box contains 300 matches , Rahul and Sachin take turns removing no more than half the matches in the box. The player who cannot move looses. What should be Rahul's first move to ensure his win if he is starting the game?
0
28/09/2018 6:10 pm
aniket prajapati 28/09/2018 7:21 pm
Series can be written as
(1-2/3) + (2/3-2/5) + (2/5-2/7) + (2/7-2/9) + (2/9-2/11)
= 1-2/11
= 9/11 option (4)
0
03/10/2018 2:41 pm
TG Team 03/10/2018 4:52 pm
a , ar , ar2 , ar3 , ar4 , …..
a + ar = 15
a ( 1 +r) = 15
a = 15/ ( 1+ r) …. (1)
Now ,
3(ar + ar2 + ar3 + ar4 +….) = a
3 [ar / (1-r)] = a
1 - r = 3r
r = ¼
from (1)
a = 12
Sum of the series : a , ar , ar2 , ar3 , ar4 , …..
a / ( 1 –r) = 12 ( 1-1/3) = 16
0
03/10/2018 3:07 pm
Hi sir, please help
0
04/10/2018 3:41 pm
Consider the sequence of numbers - 1,22,333,4444,..... where each natural number 'n' repeats 'n'times. The 2015th number in the sequence will be?
TG Team 04/10/2018 4:52 pm
If the question asks about 2015th number, then it will simply be 201520152015..... ( 2015 written 2015 times )
0
10/10/2018 11:05 am
Let D(N) denote the difference of sum of all even digits of N from sum of all odd digits of N. For example D(5678) = (5 + 7) – (6 + 8) = -2 and D(786) = (7) – (6 + 8) = -7.
Evaluate D(1) + D(2) + D(3) + …..+ D(9999).
0
4000
10000
20000
TG Team 10/10/2018 1:03 pm
0000 , 0001 , 0002 , 0003 , ........, 9999
Number of digits used : 4 x 10000 = 40000
Each digit used : 40000/10 = 4000times
D(1) + D(2) + D(3) + …..+ D(9999)= ( Sum of all odd digits used ) - (Sum of all even digits used )
= ( 1+ 3 + 5 + 7 + 9) x 4000 - ( 0 + 2 + 4 + 6 + 8) x 4000 = 4000 x 5 = 20000.
Option (D)
0
10/10/2018 3:40 pm
solution for 7,8,10
TG Team 10/10/2018 5:00 pm
Alternative Approach for 7th Question :
Put x = 2 and check whether u is 8.
Put x = 4 and check whether u is 4.
Put x = 16 and check whether u is 2 or not .
Only x = 4 satisfies the equation .
0
10/10/2018 3:54 pm
solution for questions 13,24,25,26 please.
aniket prajapati 10/10/2018 9:21 pm
there is a print error in question 25 option 1st should be (2,-1/2)
now for solution; from given equation
logx=ab logy-------------------(1)
logy=b log z--------------------(2)
logz= a logx
substituting value of log z in 2nd
logy= ab logx-------------------(3)
from 1 and 2
a2b2=1
now check options only E doesn't follow this condition
0
10/10/2018 3:58 pm
tothepoint 26/08/2019 6:23 pm
Total yearly investment of Jatinder = (20000*4)+(16000*5)+(10000*3)=190000. For this investment, he is getting 19000 profit. Hence, for Ravinder to get Rs 19200 profit, his total investment should be 192000 for the year. Therefore, his initial investment should be 192000/12=16000.
0
10/10/2018 5:56 pm
FInd the odd term
13, 21, 34, 64, 89, 144
TG Team 10/10/2018 6:04 pm
13 , 21 , (13 + 21) , ( 21 + 34) , ( 34 + 55) , ( 55 + 89) ... and so on .
Hence , 64.
0
12/10/2018 11:11 pm
If a, b, c are roots of x³ - 7x² - 6x + 5 = 0, find the value of (a + b)(b + c)(c + a).
aniket prajapati 12/10/2018 11:34 pm
a+b+c=7 .................(1)
ab+bc+ca= -6 .................(2)
abc= -5
(a+b)(b+c)(c+a)= (ab+ac+b^2 +bc)(c+a)
putting values from 1 and 2
(b² -6)(7-b)
7b²-b³ +6b-42
-(b³ -7b² -6b +42).................(3)
since b is a root of given polynomial therefore b satisfies given equation
b³ - 7b² - 6b+ 5 = 0
b³ - 7b² - 6b= -5
put in (3)
= -(-5+42)
= -37 (answer)