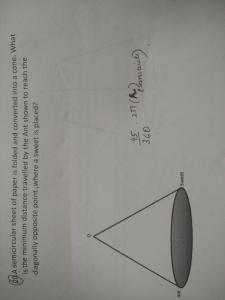
Given a, b and c are positive real numbers and log
Discriminant of a second degree polynomial with integer coefficients cannot be:
A. 43
B. 33
C. 68
D. 25
Discriminant of a second degree polynomial ax2 + bx + c ( say ) is b2 + 4ac
now square of an integer is either of the form 4k or 4k+1 so b2+4ac will never be of the form of 4k + 3.
Given a, b and c are positive real numbers and log
we know ,x3 + y3 + z3 - 3xyz = (x + y + z)(x2 + y2 + z2 - xy - yz - zx)
for given values
(log
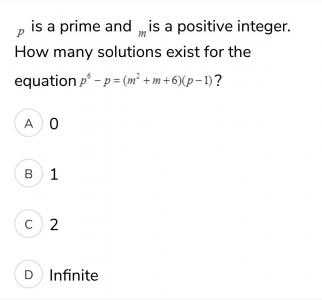
p6 - p = (m2 + m + 6)(p - 1)
p( p5 - 1) = (m2 + m + 6)(p - 1)
p ( p4 + p3 + p2 + p + 1 )(p - 1) = (m2 + m + 6)(p - 1)
p ( p4 + p3 + p2 + p + 1 ) = (m2+ m + 6)
If p is a prime greater than 2 then LHS is an odd number , but RHS is even for all integer value of m
So no solution for p> 2.
When p = 2 then m2 + m - 56 = 0 so m= -8, 7 Only one solution m=7 ; p=2
x + 1/x = - √3
Cubing both sides we get
x³ + 1/x³ + 3 ( x + 1/x) = - 3√3
x³ + 1/x³ - 3 √3 = -3√3
x³ + 1/x³ = 0
x^6 + 1 = 0. x³
x^6 = -1
x^42 + x^48 + x^54 + x ^60 + x^66 + x ^72
( -1)^7+ (-1)^8 + ( -1)^9 + ( -1)^10 + ( -1)^11 + ( -1)^12
0 .
x + 1/x = - √3
x³ + 1/x³ = 0
x^42 + x^48 + x^54 + x ^60 + x^66 + x ^72
= x^45(x³ + 1/x³) + x^57(x³ + 1/x³) + x^69(x³ + 1/x³)
= 0
16)
D = b^2- 4ac
Any square is of the form 4k or 4k+1
So D can't be of the form 4k+3 hence option 1
17. For each element listed, there is exactly one other element such that the two elements sum to 11. Thus, we can list all the 10 numbers above as 5 pairs of numbers, such that each pair sums to 11. The problem then can be solved as follows:
in any given subset with no two elements summing to 11, at most one element from each pair can be present. Thus, there are 3 ways in which each pair can contribute to a given subset (no element, the first element in the pair, or the second element in the pair). Since there are 5 pairs, the total number of ways to construct a subset with no two elements summing to 11 is 35 = 243.
97th answer is 5292 ?
Va at nth second will be = 2+(n-1)3 {since it forms an a.p with a=2 and d=3}
Vb at nth second will be = 3+ (n-1)d
Vb=10Va
3+(n-1)d= 10(2+(n-1)d)
(n-1)(d-30)= 17
since n>2
n=18 ,d=31
now find sum upto n terms of both a.p
Sa= 9(4+17*3) =495
Sb= 9(6+17*31) =9*533 =4797
total distance = 495+4797= 5292 (answer)
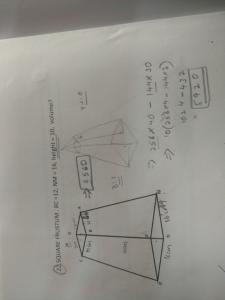
Volume of pyramid : 1/3 of area of base x height
So 1/3 x 2562 x 40 - 1/3 x 144 x 30
In order to divisible by 6.
sum of digits should be a multiple of 3 and last digit should be even.
so, when 0 is not included
2346 => 4! numbers subtract cases when 3 is at units place
4!-3! = 18 numbers
When 2 is not included : 3460 => sum 13 , not divisible by 3
When 3 is not included : 2460=> sum 12
Total 4! numbers subtract cases when 0 is at thousands place : 24 - 6 = 18
When 4 is not included : 2306 => sum 11 , not divisible by 3
When 6 is not included : 0234 => sum 9
14 numbers
Total : 14+ 18 + 18 =50 numbers
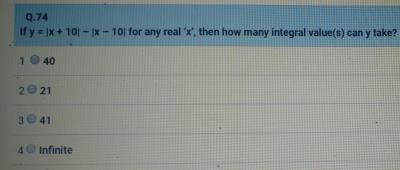
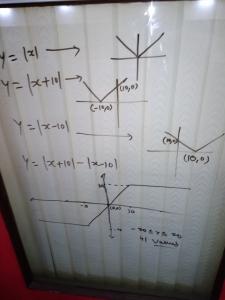
What is the value of 2 power log2 power log2 power log2 and so on?