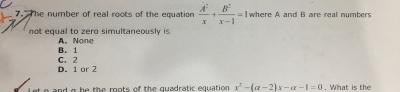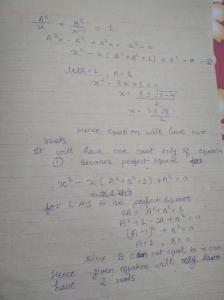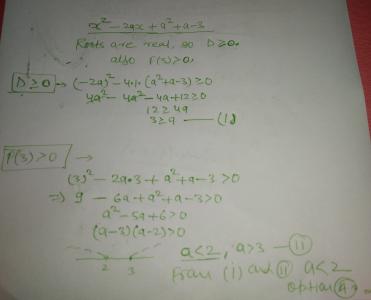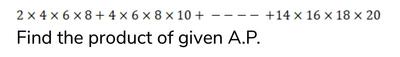22/11/2018 5:01 pm
Algebra
297
Posts
26
Users
18
Reactions
56.6 K
Views
0
22/11/2018 5:02 pm
solution for questions 10 & 12
TG Team 22/11/2018 7:27 pm
Solution to the Q. 10
a and b are roots
So , a + b = a² + b²
and ab = a²b²
=> ab(ab - 1)
i) a = 0
=> b = 0 or 1
ii) b = 0
=> a = 0 or 1
iii) ab = 1
a + 1/a = a² + 1/a²
=> a⁴ - a³- a + 1 = 0
=> (a³ - 1)(a - 1) = 0
=> a = 1 or w or w²
=> b = 1 or w² or w
So, equation are x² = 0
x² - x= 0
x² - 2x + 1 = 0 and x² + x + 1 = 0
4 such equations
TG Team 22/11/2018 7:28 pm
12
Alternative Approach:
put x = 0 in the expression x² - 2ax + a² + a - 3
it reduces to
a² + a - 3 = 0
a = -1/2 + (√13)/2 and -1/2 + √13/2
Here roots are less than 2 hence option (B) and (C) got eliminated.
Hence , Option (A ) is the correct answer .
0
23/11/2018 8:07 pm
aniket prajapati 23/11/2018 9:21 pm
16 ,b , c are in A.P
so b=(c+16)/2
c=2b-16......................(1)
16 , b+3, c+15 are in G.p
(b+3)^2= 16(15+c)
putting value of c from (1)
b^2+9+6b =16(2b-1)
b^2 -26b +25 =0
b=25 or 1
putting value of b in (1)
c=49 or 1
so smallest value is 1 hence option B
0
23/11/2018 8:11 pm
0
20/12/2018 2:55 pm
Hello sir , kindly share the solution to this problem -
An institute has 5 departments and each department has 50 students. If students are picked up randomly from all 5 departments to form a committee , what should be the minimum number of students in the committee so that at least one department should have representation of minimum 5 students? options -
A. 11
B. 15
C. 21
D. 41
E. None of the above
TG Team 21/12/2018 11:57 am
The maximum number of students can be picked from each department such that 5 students are not selected from the same department is 4.
Therefore, after 4 students from each department are selected i.e 4 x 5 = 20 , the 21st student selected will be the fifth student to be selected from one of the 5 departments.
Hence, , 20+1 = 21 students should be selected in total to ensure that at least five students from one of the departments is selected.
0
23/04/2019 6:33 pm
Gaurav Jain 25/04/2019 1:51 pm
2*4*6*8+4*6*8*10 = 4*6*8*12
+6*8*10*12 = 6*8*12*14
+8*10*12*14 = 8*12*14*16
8*12*14*16+10*12*14*16 = 12*14*16*18
+12*14*16*18 = 14*16*18*24
+14*16*18*20 = 14*16*18*44
0
22/07/2019 8:58 pm
The number of students in a university is a perfect square. In one year 2000 more students joined the original strength and the new strength is one more than a perfect square. the next year 2000 more students joined newly and the new strength of the university is again a perfect square.
Gaurav Jain 23/07/2019 1:44 pm
999^2+999+1000 = 1000^2
hence from above when 2000 is added in 999^2 , then we get 1 more than 1000^2
so initial strength is 999 students
0
22/07/2019 9:04 pm
what is the sum of all the digits of square of 99999... up to 15- digits?
Gaurav Jain 23/07/2019 1:37 pm
square of following numbers
9 81 sum of digit in square =9
99 9801 sum of digits in square = 18
999 998001 sum of digits in square = 27
by the above pattern answer for 9999...15 times will be 9*15 =135
0
22/07/2019 9:15 pm
how many perfect squares of natural numbers between 30,000-50,000 are there whose last two digits end with 81?
Gaurav Jain 23/07/2019 1:36 pm
last 2 digits 81 in all the following squares
9, 41, 59, 91, 109 and so on
now square root of 30000 and 50000 is approx 173 and 223
between 173 and 223 numbers that have 81 in the end of their squares will be
191 and 209
0
24/08/2019 10:10 pm
Harry, Hermione, and Ron are playing together with at most 40 marbles in total. All at the same time Harry passed one-third of his marbles to Hermione, Hermione passed one-fourth of her marbles to Ron and Ron passed one-fifth of his marbles to Harry. They all gave more than one marble. After this, they each had equal number of marbles. How many marbles in total could they have started with?
A. 30 B. 33 C. 36 D. 39
0
30/09/2020 10:15 pm
What is the missing number in the sequence 2,0,3,23,_____,2869?
-1
30/10/2018 6:04 pm
Find x such that |x + a| - |x - b| > 0 where a < b.
x > b
x < (b - a)/2
x > (b - a)/2
None of these
aniket prajapati 30/10/2018 6:34 pm
i m getting option 3rd
if you will open it with positive sign
x+a> x-b
a>-b this is not in options
opening with negative signs
x+a> -x+b
2x>b-a
x>(b-a)/2
which is in the option
Page 8 / 8
Prev