22/03/2018 2:20 pm
Topic starter
0
Hello sir,
Please solve the following question
49 questions & discussions are there under this sub-topic
2
10/01/2024 1:47 pm
If the diagonals of a rhombus of side 20cm are in the ratio of 3:4, then what is the area (in sq.cm) of the rhombus?
Sachin Yadav 24/01/2024 4:28 pm
@neraj-naiyar sir,
Side of the rhombus = 20 cm
Let the diagonals be 4x and 3x. They bisect each other at right angles, thereby creating 4 identical right angled triangles, with hypotenuse 20 cm.
In a single right angled triangle,
20² = (4x/2)²+(3x/2)²
400 = 4x² + (9/4)x²
400 = (25/4)x²
x=8
Total area =(1/2)(4x)(3x) = (1/2)(32)(24) = 384cm²
2
27/01/2024 1:17 pm
Q1. Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
This post was modified 1 year ago by Sachin Yadav
2
03/02/2024 2:32 pm
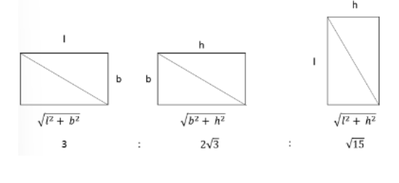
Q1. If the rectangular faces of a brick have their diagonals in the ratio 3 : 2 √3 : √15, then the ratio of the length of the shortest edge of the brick to that of its longest edge is?
A. 1 : √3
B. 2 : √5
C.√2 :√3
D. √3 : 2
0
31/03/2018 2:32 pm
ABCD is a trapezium, in which AD and BC are parallel. If the four sides AB, BC, CD and DA are respectively 9cm, 12cm, 15cm and 20cm then the magnitude of the sum of the squares of the two diagonals is:
(a) 638 (b) 786 (c) 838 (d) 648
0
31/03/2018 2:32 pm
Let the height be h. Base be 20 top be 12.
Draw perpendiculars from the edges of the top to the base.
We have left overs of the base on both the sides. call them x and y.
Now X+Y =8
Now sum of the diagonals is nothing but h^2 + (20-y)^2 + h^2 + (20-x)^2
it comes out to be 800-40(x+y)+2 h^2 + X^2 + Y^2
We have h^2+X^2 = 9^2 and h^2+ Y^2 = 15^2 and X + Y = 8
Ans = 786.
0
05/04/2018 1:23 pm
Topic starter
Hello sir,
Please solve this question:
ABCD is a trapezium, such that AB, DC are parallel and BC is perpendicular to them. If angle DAB = 45o, BC = 2 cm and CD = 3 cm then AB = ?
(A) 5 cm (B) 4 cm
(C) 3 cm (D) 2 cm
Anonymous 05/04/2018 6:19 pm
Hello Ananya,
Please find the attachment.
Draw DE perpendicular on AB,
CD = BE= 3 cm,
AE = ED = 2 cm.
AB = AE + EB = 2 + 3 = 5 cm
0
09/07/2018 10:12 pm
Find the value of x
0
21/07/2018 1:37 am
Could you please solve this question?
0
25/07/2018 10:11 pm
A dog is tied to the corner of a house with a regular hexagonal base that measures 6 ft on each side. If the rope is 12 ft in length, what is the area in square feet of the region outside the house that the dog can reach?
0
25/07/2018 10:19 pm
Both the questions, please.
TG Team 25/07/2018 11:03 pm
3.
AB = OP ( Diagonals of a rectangle )
OP = r = 36
Diameter = 2r = 72in
0
26/07/2018 12:28 am
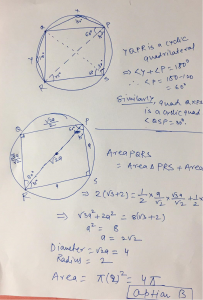
Hey sir, posting a question below. Though I've solved the question with the approach mentioned in the image (solution with blue pen), but is there any way to solve it faster? If somehow we could prove triangle PBC as a right angled triangle, it's just a 10sec question. But my question is, how could we do that?
TG Team 26/07/2018 4:58 pm
Hello Richa !
Rotate P to P' 90 degrees with centre B .
We get PP' = 6√2
So BPP' = 45 degrees
Now cosP'PC = √2/2
cosP'PC = 45 degrees too.
So , Area = BC^2 = 14^2 + 6^2 = 232 .
0
27/07/2018 6:16 pm
Hello Sir, please help.
0
01/08/2018 9:21 am
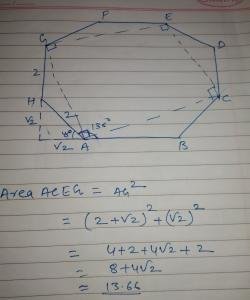
In regular octagon ABCDEFGH
Find the area of ACEG, if side of octagon is 2 cm
A. 13.24
B.12.97
C.14.18
D 13.66
0
02/08/2018 5:46 pm
Sir please help
TG Team 02/08/2018 6:32 pm
Triangle MEC ~ Triangle BEA
Area MEC / Area BEA = MC²/AB² = 1²/2²
If , Area MEC = x then Area AEB = 4x
EC : AE = 1 : 2 hence area BEC = 2x
Area [Square ABCD] = 2 [ Area ABC] = 12x
Area AEMD = 12x - 2x - x - 4x = 5x
Required ratio : x : 5x = 1: 5
Page 1 / 4
Next