02/08/2018 7:25 pm
0
Unable to solve
TG Team 02/08/2018 7:33 pm
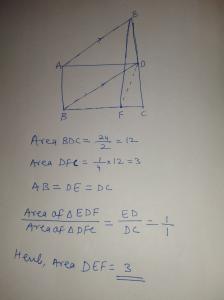
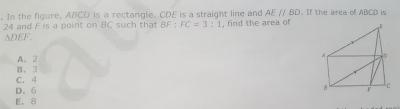Hint : Area Base Ratio - Ratio of area of triangles having base on the same line and third vertex common is equal to the ratio of length of bases of the triangles
0
08/08/2018 5:59 am
Hey Sir, help me solve this problem.
0
08/08/2018 6:30 am
aniket prajapati 08/08/2018 3:34 pm
In 2nd question.
Just square the sides given ,add them and see the sum will be square of 73
For example u can consider a triangle or sqaure or hexagon u will get same result ..
aniket prajapati 08/08/2018 4:23 pm
Sir, in third question they should tell that assuming there is no slag . shouldn't they ?
0
13/08/2018 10:16 pm
The length of 3 sides of a convex quadrilateral are 4cm, 8cm, and 16cm. How many positive integer values can the fourth side (in cm) take if no two sides have the same length?
A. 23
B. 19
C. 21
D. 24
TG Team 13/08/2018 11:14 pm
Sum of any three sides in a quadrilateral is greater than the fourth side
so 4 + 8 + 16 > n
28 > n .... (1)
also , 4 + 8 + n > 16
n > 4 .... (2)
From (1) and (2)
28 > n > 4
Hence , { 5,6,7,8,....., 27} - { 8 , 16}
21 integral values .
Richa 14/08/2018 1:03 am
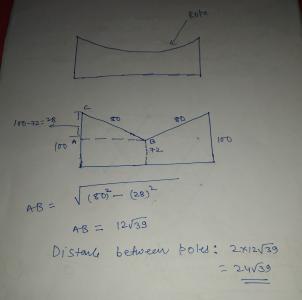
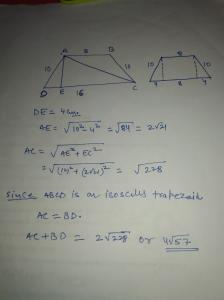
Hi Sir, thank you for this. I did it using another approach. I first divided the quadrilateral into 2 triangles and then used the property of the sum of two sides greater than the third. This way, I got the range of the diagonal of the quadrilateral and then the range of the fourth side. But I am getting a total of 19 values. Attaching my method below.
Can you please point out the mistake in my method?
0
17/08/2018 1:20 am
Sir, how do we know that A,B,E,D are concyclic points (as mentioned in the solution)?
TG Team 17/08/2018 12:33 pm
Angle DAB = 90 , Angle AEB = 90 : Angles subtended by BD are equal so points A,E,B, D are concyclic points.
0
18/08/2018 10:54 pm
A regular polygon has interior angles of 168°. How many sides does the polygon have ?
A regular polygon has an interior angle that measures 144° , and a side of which is 12 units long . What is the perimeter of the regular polygon ?
TG Team 18/08/2018 11:05 pm
Sum of all interior angles = ( n -2) × 180°
[(n -2) × 180° ]/n = 168°
(n -2 ) × 180 = 168n
12n = 360°
n = 30
TG Team 18/08/2018 11:09 pm
Alternate Approach :
Each exterior angle : 180 - 168 = 12°
We know sum of all exterior angles of a polygon is always 360°
So , 360/12 = 30 exterior angles.
Hence number of sides = 30 .
TG Team 18/08/2018 11:11 pm
For 2nd problem :
Each exterior angle 180 - 144 = 36
Number of sides = 360/36 = 10
Perimeter of the polygon : 10 × 12 = 120 units
0
25/08/2018 12:28 am
0
31/08/2018 11:35 pm
Hello sir, Please share the solution to this problem -
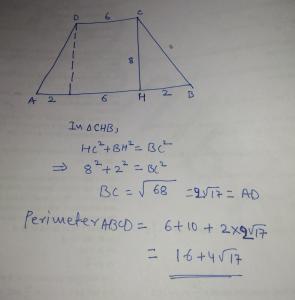
In a quadrilateral ABCD , AB is parallel to CD. AB= 8 cm , BC = 10 cm ,CD = 16 cm and AD =10 cm. Find the sum of the lengths of the diagonals.
0
05/09/2018 10:09 pm
Hello sir, please share the solution to this problem -
0
12/10/2018 10:30 pm
In a regular polygon of ‘n’ sides, a circle of radius r is inscribed and another circle of radius R is circumscribed. Which of the following is definitely true?
R/r > 1
R/r < 2
R/r ≤ 2
1 < R/r ≤ 2
aniket prajapati 12/10/2018 11:09 pm
for instance take a equilateral triangle r=a/2√3 and R=a/√3
R/r=2.................(1)
now take a square r=a/2 and R=a√2/2
R/r=√2=1.414 ...................(2)
from 1 and 2
1 < R/r ≤ 2
hence option (4)
0
13/10/2018 11:02 am
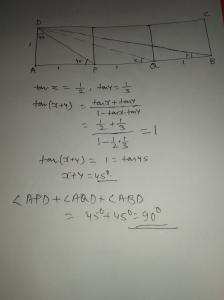
Three identical squares with bases AP, PQ, and QB are put next to each other to form a rectangle ABCD. Find the sum of the angles <APD + <AQD + <ABD.
60
75
90
120
0
14/10/2018 8:27 pm
0
19/10/2018 3:35 pm
Hello Sir , kindly share the solution to this problem -
TG Team 19/10/2018 4:44 pm
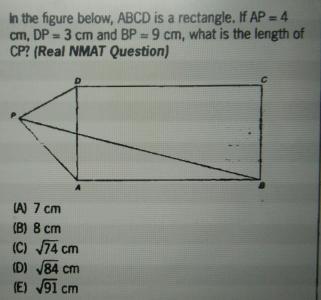
Hi Nikita ,
Please go through this link : https://artofproblemsolving.com/wiki/index.php?title=British_Flag_Theorem
This theorem is valid irrespective of whether P inside/Outside or the boundary of the rectangle .
