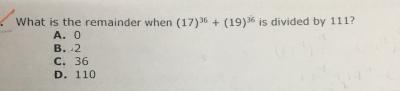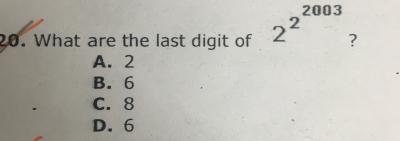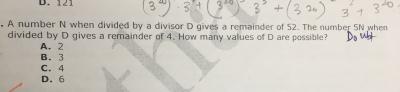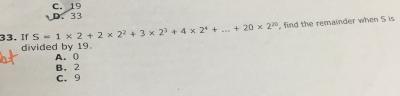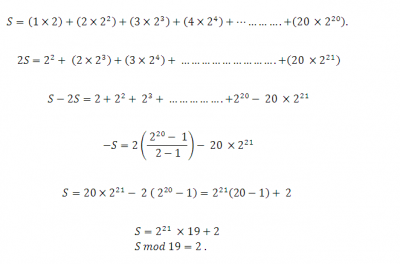Take 1075^n common
You will get 1075^(n-1) *1074
Now check options 15 will be divisible because 1075 contains 5 and 1074 contains 3
1075 contains 43
1074 contains 179 we can find it by prime factorisation
Hence 23 is not divisible
Since digits of 10digits number n sum to 45 , n should be divisible by 9
n should be divisible by 99999
10 digits number will be of type
n = 100000x + y where x is 5digit number and y is 4 or 5 digit number
n = 99999x + (x+y)
means x+y should be divisible by 99999
and because neither x > 99999 nor y>99999
x+y = 99999
x=abcde
y=pqrst
----------------------
x+y=99999
also since max numbers is 9 and 8 we cannot carry to next digit (19)
so it has to be all 9s without carry
groups
0 9
1 8
2 7
3 6
4 5
means combination is for x only. y is related
digit 1 : {1-9} 9ways
digit 2 : {digit1,0} - {digit1,9-digit1} 8 ways
digit 3 : {digit2} - {digit2.9-digit2} 6 ways
digit 4 : {digit3} - {digit3.9-digit3} 4 ways
digit 5 : {digit4} - {digit4.9-digit4} 2 ways
total ways : 9 × 8 × 6 × 4 × 2 =3456
from 1sr statement there are two possibilities...2^2*3^6 or 2^5*3^3
(considering that from 2nd statement on multiplying n with 3 or n with 2 , factors don't double or get hugely increased hence 2 and 3 are the only prime factors)
now from 2nd statement we find that 1st case in not possible hence, our n= 2^5*3^3
now u can find 6n, (6+1)*(4+1) =35
25 pages consist of 25 odd numbers and 25 even numbers
So there sum should always be odd
Hence 1900 an even sum is never possible.
a=10x+y
b=10y+x
a+b = 11(x+y)
x+y =11 for a+b to be a perfect sqaure and a and b to be a two digit nos.
Values can be
(9,2) (8,3) (7,4) (6,5)
Hence 4 pairs
Hi Aniket, thankyou for the solution.
But since the question is asking for ordered pairs, shouldn't it be 8 pairs? (9,2) (2,9) (8,3) (3,8) (7,4) (4,7) and (6,5) (5,6)?
Please suggest if im going wrong somewhere
put 17 as (2-19) -19 to the power 36 and 19 to the power 36 cancels out hence the answer is 2
(Any odd number )^ (4k ) ends with 1 or 5
*( odd multiples of 5 )^(Any natural number ) ends with 5.
(Any even number )^4k ends with 6 or 0
*(Even multiples of 5)^ any natural number => 0
________________________________________
Here 2^2^2002
2 ^ ( 2^2002)
2^ ( 2 x 2 x 2 ..... 2002 times )
=> 2^4k
Hence , the last digit of 2^2^2002 => 6
N = DQ + 52
=> 5N = D (5Q) + 52 x 5
5N = 5DQ + 260
Also 5N = Dx + 4
So , D divides (260 - 4) i.e 256
hence , All factors of 256 > 52 .
[ 256 , 128 and 64 ]
How many two digit numbers are there such that last two digits of this number remain unchanged when it is cubed?
this could only be possible if both digits must be same so nos. are
33,44,55,66,77,88,99
total =7 (answer)
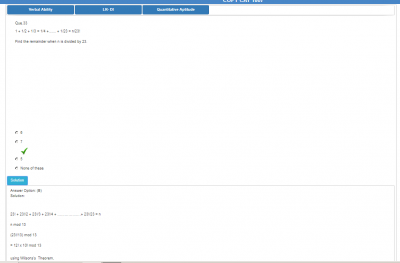
1 + 1/2 + 1/3 = 1/4 +....... + 1/23 = n/23!
Find the remainder when n is divided by 23.
What is the remainder when 13!^14!^15! Is divided by 16?
1 x 2 x 3 x 4 x 5x ...... x 13 i.e 13! is a multiple of 16 .
Hence 13! raised to any power would be a multiple of 16.
Therefore the remainder will be 0.
If n=539x2^18 and m=9x2^13 then the remainder when n is divided by m is?
What are the last non zero digit of 36!-24!?
N*190/100 = N*19/10
No. N should have 19 and 10 so that when it is increased by 90% it becomes a perfect square hence it will be multiple of 190
Possible values can be (190,380,570,760,950)
Only 190 and 760 will give perfect sqaure when they are increased by 90%
190/7 gives remainedr 1 and 760/7= gives remainder =4
Sum of remainder= 4+1 =5 answer