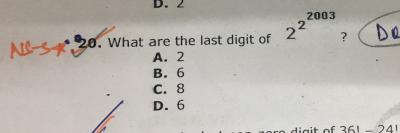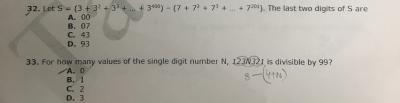If A = 71421 .......... 98 105 112 .........189 196,
what is the remainder when A is divided by 9?
(A) 1 (B) 3 (C) 7 (D) 5
Can we use the concept of digital sum of an A.P. here?
If we add 7+14+21...196, will it be same as the digital sum of A? And since we have to find the remainder when divided by 9, we can anyway eliminate the 9s while adding.
To obtain the 9’s remainder of any number, we can proceed in a number of ways.
At one extreme, we can consider the given number itself as a single quantity.
As the other extreme, we can focus on each individual digit and add them all up.
As an intermediate approach, we can ‘fragment’ the number in any convenient way and consider the fragments.
In the given question, the third approach is the most convenient.
i.e. instead of A itself (or the individual digits of A) we consider B = 7 + 14 + 21 + … + 189 + 196 = 7(1 + 2 + 3 + … + 27 + 28) = 7(14)(29)
The 9’s remainder of the product of several numbers is the product of the 9’s remainders of the numbers.
∴ The required remainder is the remainder of 7(5) (2) or 7
If it is known that B is a multiple of 5 and C an odd number, then which of the following is possibly A’s unit digit, given that
3A2 + 2B2 = C2
Ans: 5
2B^2 will give unit digit 0
hence 3A^2= C^2 (unit digit will be same)
A^2 = (C^2)/3
since C is a odd no. C^2 can have unit digit 1,5,9
if we put 9 as C^2 then on dividing it with 3 we will get unit digit 3 which is not a square's unit digit and if we put 1 then on dividing with 3 we get 7 which is also not a square no.'s unit digit so only left is 5 if we put that we will get unit digit of A as 5 hence answer
y² + 8y - 857 = x²
y² + 2• y • 4 + 16 - 857 -16 = x²
( y + 4)² - 873 = x²
( y +4)² - x² = 873
p² - x² = 873
( p - x) ( p +x) = 1 • 873
( p - x) ( p +x) = 3 • 291
or 9 × 97
p = 437 or 147 or 53
y = 433 or 143 or 49
Now find sigma f(y) .
If four numbers are in AP .
Then,
their product + ( Common difference )⁴ is always a perfect square.
Hence , 2⁴ => 16
Option ( D)
remainder when 17! is divided by 23?
We can write 50 as ( 51- 1)
( 51 -1)^60 ^70 divided by 3
( -1)^60^70 => (-1)^even = 1
Hence , 3k + 1
5! = 120
last two digits of 6! => 6 x 20 = ___20
last two digits of 7! => 7 x 20 = ___ 40
last two digits of 8! => 8 x 40 = ___ 20
last two digits of 9! => 9 x 20 = ___ 80
last two digits of 10! => 00
Last two digits of N :
1 + 2 + 6 + 24 + 20 + 20 + 40 + 20 + 80 + 00 = __13
N^N /4 => 13/4 => 1
(Any odd number )^ (4k ) ends with 1 or 5
*( odd multiples of 5 )^(Any natural number ) ends with 5.
(Any even number )^4k ends with 6 or 0
*(Even multiples of 5)^ any natural number => 0
________________________________________
Here 2^2^2002
2 ^ ( 2^2002)
2^ ( 2 x 2 x 2 ..... 2002 times )
=> 2^4k
Hence , the last digit of 2^2^2002 => 6
take 10! common
N = 10! ( 1 + 11 x 12 + 11 x 12 x 13 x 14 +.........)
= 10! x ( an odd number )
hence the highest power of 2 in N = highest power of 2 in 10!
i.e [10/2 ] + [5/2] + [2/2]= 8
33.
In order to divisible by 99,
123N321 should be a multiple of 9 and 11 .
1 + 2 + 3 + N + 3 + 2 + 1 = 12 + N should be a multiple of 9
Only possibility N = 6
When N = 6
1236321
(1 + 3 + 3 + 1) - ( 2 + 6 + 2) = -2
So 1236321 is not divisible by 11.
Hence , no solution.
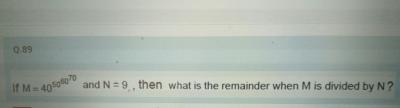
The arithmetic mean of the nine numbers 9,99,999,9999,…..99999(9times) is a number M. What is the remainder when MM is divided by 13?
Find remainder when (2222^5555+ 5555^2222)/7.
The remainders when 5555 and 2222 are divided by 7 are 4 and 3 respectively. Hence, the problem reduces to finding the remainder when (4) 2222 + (3)5555 is divided by 7.
Now (4)2222 + (3)5555 = (42)1111 + (35)1111 = (16)1111 + (243)1111. Now (16)1111 + (243)1111 is divisible by 16 + 243 or it is divisible by 259, which is a multiple of 7.
Hence the remainder when (5555)2222 +(2222)5555 is divided by 7 is zero.
What is the unit digit of 1273^122! ?
31 => 3 unit digit 3
32 => 9 unit digit 9
33 => 27 unit digit 7
34 => 81 unit digit 1
35 => 243 unit digit 3
36 => 729 unit digit 9
…………………………………
……………………………….
34 always ends with 1
unit digit of 1273122! is same as the unit digit of 3122!
34k => 1