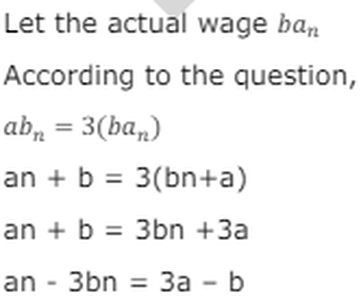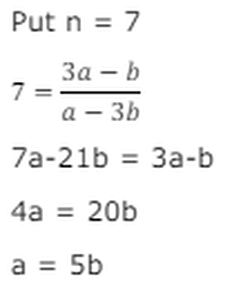06/11/2018 6:29 pm
Number system
73
Posts
20
Users
3
Reactions
32.8 K
Views
0
The sum of 20 numbers(may or may not be distinct)is 801. What is their minimum LCM?
aniket prajapati 07/11/2018 1:55 pm
Just try with options.
Start with 36.
801 = 36*22 + 9.
But we need 20 numbers only. So rule out 36.
Take 42.
801 = 42*19 + 3.
LCM(42,3) = 42. (answer)
0
13/11/2018 6:02 pm
Find the total number of even factors of the L.C.M. of first 25 natural numbers.
This post was modified 6 months ago 2 times by TathaGat
TG Team 13/11/2018 6:36 pm
The highest power of 2 in LCM of first 25 natural number is 4, as 16 = 2^4
The highest power of 3 in LCM of first 25 natural number is 2 , as 9 = 3^2
Highest power of 5 , 5^2
Similarly highest power of 7, 11, 13 , 17 , 19 , and 23 = 1
LCM : 2^ 4 x 3^2 x 5^2 x 7 x 11 x 13 x 17 x 19 x 23 .
No of even factors : 4 x 3 x 3 x 2 x 2 x 2 x 2 x 2 x 2 = 2304
0
14/11/2018 9:03 pm
For how many integers, n, the expression n2 + n + 4 is a perfect square?
0
24/06/2019 12:08 am
Q.How many natural numbers between 1 and 100 have exactly 4 factors?
Gaurav Jain 25/06/2019 10:38 am
For exactly 4 factors . Result comes from following 2 forms
2*2---> corresponds to the number of form (a*b) where a,b are primes
and 4 ---> corresponds to the number of form (a^3)
Now let's take each form one by one
a*b form
2*3, 2*3, 2*5 ...........2*47 (14 numbers) (14 primes from 3 to 47)
then 3*5, 3*7,3*11........ 3*31 (9 numbers) (9 primes from 5 to 31)
then 5*7, 5*11.......5*19 (5 numbers)
then 7*11, 7*13 (2 numbers)
total number of this form = 30 numbers
next is a^3 form
only 3 numbers are there 2^3, 3^3, 4^3
so total 33 numbers have exactly 4 factors
0
16/11/2019 11:14 pm
Gaurav Jain 14/01/2020 7:20 pm
product is an integer, hence x and y must take same value.
now first factorize 2016
2016= 63*32
so we can take the above expression as
32k(8^2-p)
now p could be such that inside we are left with a factor of 63.
Hence when p =43 , we are left with 21 the k will become 3
and p=61, then we are left with 3, then k will become 21.
These are the only 2 values hence sum of values of p is 104
0
16/11/2019 11:17 pm
Gaurav Jain 14/01/2020 7:25 pm
median is the middle position
Now when increase of 10 changes the avg by 2. Hence there are 5 terms.
10, m-4, m , 32, 32
m is in the middle and m-4 immediate left. because in the second case when m-8 is taken instead m, then the median is m-4.
now sum of the terms should be 22*5= 110
hence m+m-4 = 36
hence m = 20
0
02/06/2024 5:58 am
Find the sum of the sum of even divisors of 96 and the sum of odd divisors of 3600 ?
TathaGat 02/06/2024 5:59 am
96 = 25x3; Sum of even divisors of 96 = (21+22+23+24+25)(30+31) = 248=
3600=24x32x52; Sum of odd divisors of 3600 = (30+31+32)(50+51+52) = 403
Ans = 403+248 = 651
0
02/06/2024 6:04 am
Find the sum of divisors of 544 which are perfect squares.
0
02/06/2024 6:12 am
In a 3 digit number, the cube of the first number exceed their product by 2, the cube of the second number is smaller than their product by 3, and the cube of the third number exceeds their product by 3
A)3^(1/3) B)9^(1/3) C)2 D)any of these
TathaGat 02/06/2024 6:13 am
Let a, b, c are the 3 digits of that number.
a3 = (abc + 2), b3 = (abc - 3), c3 = (abc + 3). Multiply all three equations and keep abc = x.
x3 = (x + 2)(x - 3)(x + 3) --> 2x2 - 9x - 18 = 0 --> (2x + 3)(x - 6) = 0 --> x = -3/2 or x = 6. Taking abc = 6 and noting that b is the smallest number b3 = 6 - 3 = 3 --> b = 31/3
0
02/06/2024 6:20 am
Find the highest power of 12 that will divide ( 536 - 1)is?
1) 1
2) 2
3) 3
4) 4
TathaGat 02/06/2024 6:21 am
Hello Anu
Find the solution:
536 - 1 = 2518 - 1 = (24 + 1)18 - 1 = 2418 + 18 x 2417 + ... + 18 x 24 + 1 - 1 = 122k.
OR
536 - 1 = (4 + 1)36 - 1 = 122k.
So highest power of 12 that will divide the expression is 2
0
02/06/2024 6:24 am
Q: 523abc is divisible by 7, 8 and 9. Then a x b x c is equal to?
TathaGat 02/06/2024 6:24 am
Hello Anu,
Since 7,8 and 9 are co-prime, the number which is divisible by 7,8 and 9, must also be divisible by their L.C.M i.e. by 504.
Now let's have a look at the given number, 523abc. It should lie between 523000 and 523999.
The multiples of 504 lying in this range are 523152 and 523656. Two possible values of abc are 152 and 656.
a,b and c are distinct, so abc must be 152, hence a x b x c = 1 x 5 x 2 = 10
0
02/06/2024 6:29 am
For how many integers x4 + x3 + x2 + x + 1 is a perfect square?
0
02/06/2024 6:30 am
10000! =(100!)^k ×p where k and p are integers. What can be the maximum value of K?
Neraj (TG) 04/06/2024 1:04 pm
The key here are the prime numbers. K should be selected in such a way that it will depict the value of the highest power of the largest prime number before 100 which is a factor of 10000!. The largest prime number below 100 is 97 and the highest power of 97 in 10000! is 104.
→ But the highest power of 2 in 10000! is 103 This step needs to kept in mind Hence, 103 is the highest power of 100! in 10000!
0
02/06/2024 6:30 am
On planet Mars the people use a certain number system to the base 'n' (n>2) , kyes a resident of the planet, one day received thrice of his daily wage because the digits of this wage, which was a 2 digit number, were reversed.
Q1. What is the least possible value of n?
Q2. What is the second least possible value of n?
Q3. If n is least possible value then what is the wages that kyes receives on a normal day (in base n)?
Q4. If the base system that is being used on the mars is the second least possible value of N then what is the sum of all the value of wages that kyes can receive for his work (in base n)?
0
02/06/2024 6:32 am
(Data sufficiency question)
Is X divisible by 15?
I. X is a number formed by writing ten consecutive natural numbers side by side.
II. X is the number formed by multiplying the factorials of three consecutive natural numbers.
Sir, I think both the statements combined are sufficient to answer the question, since the number of digits in X is at least 10. So the three consecutive natural numbers taken must have been greater than 5? But the answer is that even together they are insufficient. Why so?
Neraj (TG) 09/06/2024 5:46 pm
We can't say that number formed by ten consecutive natural numbers side by side will be divisible by 15 or not,
so, stetement I is insufficient.
According to statement II, we have
1!×2!×3! , 2!×3!×4! , 3!×4!×5! here, factorial of three consecutive number can be any number which may or may not include 5 in it, it may or may not be divisible by 15 always.
Hence, Both the statements are insufficient.