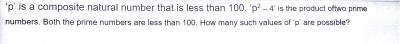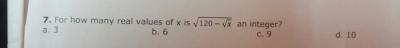14/02/2018 11:22 am
Topic starter
1
Post questions based on Integral Solutions in this forum
This topic was modified 6 months ago by TathaGat
19 questions & discussions are there under this sub-topic
1
07/03/2018 7:09 am
For how many ordered pairs (a,b) where a,b are non-negative integers satisfy the following equation:
cube root a + cube root b = cube root of 4160
TG Team 04/07/2018 3:58 pm
Hello Apoorva!
x⅓ + y⅓ = 4160⅓
a• (65)⅓ + b ( 65)⅓ = 4 • (65)⅓
a + b = 4
( 0, 4) ( 4, 0) ( 1 , 3) ( 3 , 1) ( 2 , 2)
5 ordered pairs
1
03/07/2018 7:13 pm
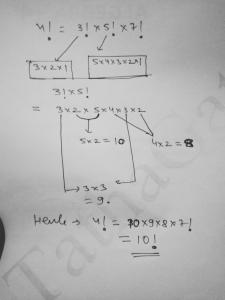
what is the value of n if value of n! = 3! *5!*7!
TG Team 03/07/2018 8:48 pm
Hello Nishant!
3! × 5! × 7!
3! × 5! = 3 × 2 × 5 × 4 × 3 × 2 = 10 × 9 × 8
Hence n ! = 10 × 9 × 8 × 7! = 10!
1
01/08/2018 9:59 pm
Sir please solve this question.
TG Team 01/08/2018 11:28 pm
P² - 4 =( P - 2)( P +2)
Here , P - 2 and P + 2 are primes . [ Difference between primes => P + 2 - ( P -2) = 4 ]
7 and 11 => P = 9
13 and 17 => P = 15
19 and 23 => P = 21
37 and 41 => P = 39
43 and 47 =>P = 45
67 and 73 => P = 69
79 and 83 => P = 81
7 values.
1
15/08/2018 10:56 pm
p is a prime number and m is a positive integer. How many solutions exist for the equation:
p^6 - p=(m^2 + m + 6)(p-1) ?
Hello Manish,
p6 - p = (m2 + m + 6)(p - 1)
p( p5 - 1) = (m2 + m + 6)(p - 1)
p ( p4 + p3 + p2 + p + 1 )(p - 1) = (m2 + m + 6)(p - 1)
p ( p4 + p3 + p2 + p + 1 ) = (m2+ m + 6)
If p is a prime greater than 2 then LHS is an odd number , but RHS is even for all integer value of m
So no solution for p> 2.
When p = 2 then m2 + m - 56 = 0 so m= -8, 7 Only one solution m=7 ; p=2
1
29/08/2018 5:47 pm
Hi sir, this is a question from CopyCat-3
My doubt is-- S(n) gives the sum of k and not digital sum, right? Had it been digital sum, then S(555) were equal to 6 and not 15, as stated in the question.
So, 2 digit number n where S(n)=5 can be only 14,23,32,41&50. How is S(59)=5?
If S(555)=15, then S(59) should be equal to 14 and not 5, right?
Please help.
aniket prajapati 29/08/2018 6:12 pm
S((n)) =S(S(n)) now S((59)) will give answer 5 and now solve the question
1
21/10/2018 1:12 am
Sir, is there any easy way to solve this?
aniket prajapati 21/10/2018 10:30 am
I can suggest this
Bdw it is a great question
there are 9 1-digit numbers(9)
there are 90 2-digit numbers(180)
there are 900 3-digit numbers(2700)
and 9000 4-digit numbers(36000)
writing them all gives us 38889 digits.
so the 38890th digit is 1 of the number 10000, the first 5 digit number.
from here on, for the next 10000 numbers (or 50000 digits), each 5th digit would be 1. so 1 is the 38890th digit and 38895th digit etc... and also the 40000th digit.
1
23/10/2018 12:07 am
How many positive integral pairs of (x, y) satisfy y2 = x4 + x2 + 1?
aniket prajapati 23/10/2018 10:31 am
x^4 + x^2 +1 -y^2 =0
Since both roots are +ve c/a >0
1-y^2>0
1>y^2
So no possible value of y to be integer
Hence no such pairs
1
24/10/2018 11:23 am
TG Team 24/10/2018 11:57 am
120 - y is a perfect sq
y can take 10 different values ( All perfect squares less than 120)
so, 10 different values for x
1
24/10/2018 11:26 am
TG Team 24/10/2018 2:15 pm
first term : 1
Sum of first 3 terms : 2
Sum of first 5 terms : 3
Sum of first 7 terms : 4
......................................
Sum of first n terms : 2016
n = 2 x 2016 -1 = 4031
Sum of the digits : 4 + 0 + 3 + 1 = 8
0
24/10/2018 11:25 am
TG Team 24/10/2018 3:42 pm
Denominator ( a - b)^3 is a multiple of 3 so ( a-b) must be a multiple of 3 Option (C).
0
04/11/2018 4:24 pm
1/a+1/b+1/ab=1/n, where a and b are prime numbers and n is a whole number. Find a^2+b^2+n^2
1. 6
2. 10
3. 3
4. None of these
I got a and b as 2 and 3, and n=1, so the answer comes 14 which is none of these. But, the given answer is 6. How?
0
17/11/2018 8:27 pm
How many four digit positive integer divisible by 7 have property that, when the first and last digit is interchanged, the result is a (not necessarily four digit) positive integer divisible by 7?
TG Team 18/11/2018 12:20 pm
ABCD – DBCA
1000A + 100B + 10C + D – ( 1000D + 100B + 10C + A)
999A – 999D
999( A-D)
999 is not divisible by 7 . so ( A – D) should be a multiple of 7.
(A- D) = ( 9 – 2) , ( 8 -1 ) , ( 7-0), ( 2 – 9) ,( 1-8) , and ( 1 -1) , ( 2-2) ,…., ( 9 – 9) total 9 + 5 = 14 cases
Now for each of these 14 cases there are 15 multiples of 7 .
[ 1. 9002 , 9072, 9172, ……., 9982 ( 15 numbers )
2. 8001 , 8071, ……….., 8981 ( 15 numbers ) similarly others ]
Hence Total : 14 15 = 210 such numbers .
0
02/04/2019 11:43 pm
all the page numbers from a book are added, beginning at page 1. However one page number was added twice by mistake. the sum obtained was 1000. Which page number was added twice?
Gaurav Jain 03/04/2019 1:41 pm
n*(n+1)/2 = approx less than 1000
n(n+1) <2000
square root of less than 2000 is 44^2 = 1936
so again , if all the numbers till 44 are added then the sum is following
44*45/2 = 990
Hence 10 was added twice
0
02/04/2019 11:47 pm
Swadesh threw five standard dice simultaneously. He found that the product of the numbers on the top faces was 216. which of the following could not be the sum of the numbers on the top five faces?
1. 17
2. 18
3. 19
4. 20
Gaurav Jain 03/04/2019 2:22 pm
Difference cases are
1*1*6*6*6 sum = 20
2*1*3*6*6 sum = 18
2*2*3*3*6 sum = 16
1*4*3*3*6 sum = 17
Hence 19 cannot be the sum
Page 1 / 2
Next