Permutation and combination

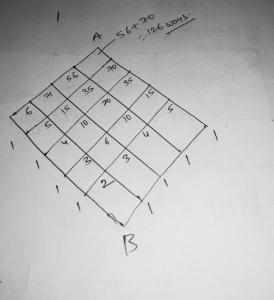
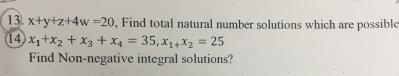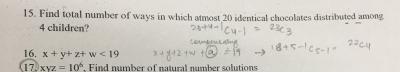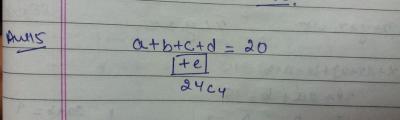shortest (1) and tallest (8) women are fixed:
XXX8
1XXX

2 and 7 have two options, so total 4 patterns:

1:
2xx8
1xx7

|2468| |2568|
|1357| |1347|

2.
2x78
1xxx

|2478| |2578| |2678| 
|1356| |1346| |1345|

3.
xxx8
12x7

|4568| |3468| |3568|
|1237| |1257| |1247|

4.
xx78
12xx

|3478| |3678| |3578| |5678| |4578| |4678|
|1256| |1245| |1246| |1234| |1236| |1235| 

14 options.

Answer: B. 

TTT | AAAHG

_ A _ A _ A _ H _ G_:  Arrange these letters in 5!/3! i.e 20 ways 

space among these letters : 6 . 

Select any three spaces in 6c3 ways 

Hence , 6C3 x 20 = 400 ways . 

6th .

other than these 3, there are 5 persons. between these persons there are 6 gaps. the chosen 3 can be anywhere in these 6 gaps , So 6C3 = 20 ways . 

5th 

ABCD 

B > C > D. 

A can take 9 values . ( 1, 2, 3, 4,...., 9) 
For D = 1 , select B and C from ( 2 , 3, 4, ... 9) in 8C2 ways . 
For D = 3 , select B and C from ( 4 , 5 , ...., 9) in 6C2 ways 
Similarly for D =5 , 7 , 9 there are 4C2 , 2C2 and 0 ways respectively . 

Hence total : 9 x ( 8C2 + 6C2 + 4C2 + 2C2 ) = 50 x 9 = 450 Numbers . 

Solution to the question 36 . 

Let box 1 contains black, others white. Similarly box 2 black, others white..so on. Therefore, case of one box containing black has 6 possibilities.
Similarly 1 and 2 contain black , rest white. 2 and 3 contain black, rest white..and so on. So 5 possibilities

Similarly for 3, 4,5 and all 6 boxes containing black balls.
So total
6 + 5+4+3+2+1 = 21 possibilities

30th part (iii)

three cases will be formed with atleast 2 girls 

(2G,2B)   (3G,1B)  (4G,0B)

5C2*4C2 +5C3*4C1 +5C2*4C0

10*6+10*4+5=105 WAYS

Alternate Approach : 

Total : 9C4 = 126 

remove cases when there is no girl and 1 girl. 

So , 126 - 4C4 - 5c1 x 4C3 = 126 - 1 - 20  = 105

47th 

Number of ways of selecting 3 different letters:
=4C3=4 ways

Number of ways to select 2 similar and 1different letter:
=4C1×3C2=12 ways

Number of ways select 3 similar letter =2 ways

total=4+12+2=18 ways

in other questions also you have to make cases and then add them

41st

No of groups = 4
Towns in each group = 3

For towns belonging to the same group.
Lets say a1, a2, a3.

Each requires 3 connections with other town in same group.
a1 to a2 = 3 connections (same as a2 to a1)
a1 to a3 = 3 connections (same as a3 to a1)
a2 to a3 = 3 connections (same as a3 to a2)

We have total of 9 connections required in same group. 

4 groups --> So total no of connections = 4*9 = 36

Now, for connections between the groups = a,b,c,d

a1 to (b1,b2,b3) = 3 connections
a1 to (c1,c2,c3) = 3 connections
a1 to (d1,d2,d3) = 3 connections
Total connections = 9

Similarly a2 and a3 to other groups will have 9 + 9 = 18 connections.

As explained above, From group 'a' to other groups b,c,d = 9*3 = 27 connections
From group 'b' to group c,d = 9*2 = 18 connections
From group 'c' to group d = 9*1 connections

So total no of connections required = 4*9 + 9*(3+2+1) = 90 connections.

Ans 13

here introduce the fifth variable to minimize the value of other four variables.

ans 15

there is a general formula to solve this question

4n^2+2

therefore 4*15*15 + 2= 902

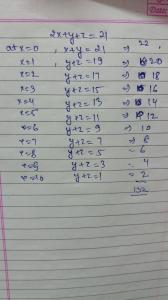
Three Cases 

(1) none of them 0 . 

x + y + z = 10 => `14C2 

14C2 x 8 = 728 cases 

(2) One of them 0. 

3C2 x 14 = 42 

42 x 4 = 168 cases 

(3) Two  0. 
3C1 x 1 

3 x 2 = 6 cases 

Total : 6 + 168 + 728 = 902 Solutions . 

Some important results : 

Total Number of ontegral solution : 

| X | = n ;  2

| X | + |Y | = n ; 4n 

|X | + |Y | + |Y | = ; 4n² + 2 

|W | + |X| + |Y| + |Z| = n ; 8n/3 × (n² + 2) 

(a)

For 4 dices being thrown sum or we can say outcomes can be:

4,5,6,………………14……………..,22,23,24

We also know that these are equally spaced and aligned with symmetry.

Mid point is (24+4)/2 = 14. The left side of the mid point is mirror image of the right part.

No of ways to get 19=(14+5) = no of ways to get (14-5)= 9

9-1C4-1= 8C3=56 ways 

same can be done with b part also

(6-a) + (6-b) + (6-c) + (6-d) = 19 

a + b + c + d = 24 - 19 = 5 

Hence , 8c3 = 56 ways . 

____________________________________
(6-a) + (6-b) + (6-c) + (6-d) = 18 

a + b + c + d = 6 
Total : 9C3 solutions 

Remove cases when a or b or c  or d =6. ( 4 ways ) 

Hence , 80 ways , 

8empty seats left (denoted by O)

like O O O O O O O O

there are 7+2=9 interspace to place the 6 groups,

this can be done in 9C6

if the persons' order is alterable,

then the answer is 9C6 * 12!

consider all outcomes for sum to be 11 following cases are there

(6,4,1) =3! ways= 6 ways

(6,3,2)=3!=6

(5,5,1)=3!/2!=3

(5,4,2)=3!=6

(5,3,3)=3!/2!=3

(4,4,3)=3!/2!=3

total 27 ways 

Alternatively : 

( 6 -a ) + ( 6 - b) + ( 6 - c) = 11 

a+ b + c = 7 

9C2 = 36 solutions 

Remove cases when a or  b, or c greater than 5 . 

a' + 6 + b + c = 7 

a' + b + c = 1 => 3C2 i.e  3 solutions.

36 - 3 × 3 = 27 ways . 

Two cases possible : 

(1) 3 , 3, 1 => 3C2 x 7C3 x 4C3 x 1 = 420 ways 

(2) 3 , 2, 2 => 3C2 x  7C3 x 4C2 x 2C2 =  630 ways

Total : 420 + 630 = 1050 ways 

14. 
 E is four steps ahead of A. So it is not possible to reach E from A in (2n - 1) i.e. odd number of steps. Hence Option ( A) 

15.
is it 33 ? 

I am not sure of the answer. But could you please share you approach?

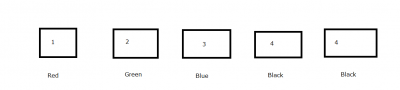
Three cases:
(1) When two fours go to black boxes. 

for 4's => 1 way , for 1 , 2, and 3  there are 3! ways . 

(2) When one four goes to one black box. 

for the 2nd black box we have 3C1 ways.  for remaining three cards and three boxes there are  3! ways so 3C1 x 3! i.e 18 ways. 

(3)When no fours goes to black boxes , for black boxes we can select 2 cards from 1 , 2, 3 in 3C2 ways , for remaining three cards there are 3! / 2! ways i.e = 3 

Hence 6 + 18 + 9 = 33 ways.