27/10/2018 2:01 pm
PnC , Probability
52
Posts
15
Users
5
Reactions
9,090
Views
0
Please help me with the approach for both the questions.
TG Team Topic starter
27/10/2018 2:31 pm
The probability of 0 hits out of n is nCo × (1/2)^n and 1 hit out of n is nC1 × ( 1/2)^n
Probability of destroying > 0.99...... = 1-{nC0×(1/2)^n + nC1×(1/2)^n } > 0.99
=> 1 - ( n +1)/2^n > 0.99
=> 1- 0.99 > ( n +1)/2^n
Smallest n = 11.
0
01/11/2018 4:38 pm
each of 2 persons tosses three fair coins. The probability that they obtain the same no of heads is?
number of possible outcomes when 3 fair coins are tossed => 2^3
{ TTT , TTH , THH , HHH , HHT , HTT , HTH , THT}
Probability of A getting 3 heads => 1/8
So probability that both will get 3 heads is 1/8 x 1/8 = 1/64
Probability of A getting 2 heads => 3/8
so probabilty that bothwill get 2 heads => 3/8 x 3/8
Similarly probability of getting 1 heads => 3/8 x 3/8
and probabilty of getting o heads => 1/8 x 1/8
2/64 + 18/64 = 5/16
0
01/11/2018 4:54 pm
2 persons a and b throw a coin alternatively till one of them gets head and wins the game . what are their respectively probability of winning?
0
03/11/2018 4:28 pm
A fanne-khan Mathematician was asked to solve for the roots of the function,
F(x) = x4 – x3 + 2x2 -4x – 8
If the mathematician gave only one answer, what is the probability that his answer was the lowest possible real root given that his answer was correct and a real root of the function indeed?
0.5
0.33
0.25
None of these
TG Team Topic starter
03/11/2018 6:53 pm
x⁴ - x³ + 2x² -4x -8 = 0
( x +1) ( x -2) ( x² +4) = 0
x = -1 , 2 ± 2i
Two real , two imaginary roots.
Probability of getting smallest real root : 1/2:
0
04/12/2018 3:25 pm
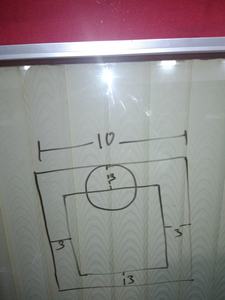
A coin of radius 3 cm is randomly dropped on a square floor full of square shaped tiles of side 10 cm each. What is the probability that the coin will land completely within a tile?
TG Team Topic starter
05/12/2018 2:46 pm
If the centre of the coin falls anywhere on smaller square , the coin lies entirely within the bigger square (tile). The probability that the coin lies entirely within a tile is : (area of smaller square)/( area of the bigger sqaure ) = 16/100 = 0.16
0
18/12/2018 5:55 pm
A teacher selects 23 speakers to speak in the class. What is the probability that A is followed by B and B is followed by C?
Sir, does this mean that they are speaking consecutively or we will consider it to be not necessarily consecutive(and this probability is 1/6)?
0
24/12/2018 11:41 am
Two points A and B are picked on a circle with a unit radius. What is the probability that the chord AB has at least length 1 unit?
0
07/08/2024 6:49 pm
Sundernagar is the only human colony on the Moon. Population of Sundernagar is 16,000, out of which 50% are children and remaining 50% are adults. Out of the adults in Sundernagar, 75% men and 50% women are married. How many people in Sundernagar are married if it is known that there are no widows/widowers and every married person has only one spouse and none of the children are married?
1.2400
2.4200
3.4800
4.8400
-1
15/10/2018 10:24 pm
solution for question 48 please
aniket prajapati 15/10/2018 10:42 pm
48th
Assuming the seating assignments are fixed, the problem is tantamount to arranging 17 blue chairs and 33 green chairs in a circle so that no two of the green chairs are adjacent. We will solve the problem for a line, then adjust our answer because chairs are arranged in a circle.
Line up 17 blue chairs. This creates 18 spaces, 16between successive blue chairs and two at the ends of the row. Choose three of the spaces in which to place a green chair. This can be done in (18C3)ways.
However, we have counted selections in which both the first and last chairs are green. If both ends are selected, there are 16 remaining spaces in which we place the third green chair. Hence, there are 16 linear arrangements in which no two of the green chairs are adjacent in which there is a green chair at both ends of the row. Since we will be joining the ends of the row to form a circle, these arrangements must be excluded.
Therefore, the number of ways of circular arrangements of 17 blue chairs and 33 green chairs so that no two of the green chairs are adjacent is
18C3 - 16C1= 3*17*16-16 =16*50=800 (answer)
Page 2 / 2
Prev