Time and Distance

Hello Samyak , 

A __2x__ B ______5x_____C 

A __2y__ B __y__D________C 

2y = 2x => x = y 

Now , DC = 4x 

Distance traveled by Xavier => AC + CD = 11x 

Distance traveled by Yohana => BC + CD = 5x + 4x = 9x 

Time taken by Xavier and Yohana is same here Hence ratio of speeds = Ratio of distance travelled  

i.e 11x :9x = 11 : 9 

Let the original speed  be V km/hr an original time taken => T hr  . 

Now, VT = ( V +3) ( T -2) 

=> VT = VT - 2V + 3T - 6 = VT 

3T - 2V = 6..... (1) 

also , VT = ( V - 4) ( T +5) 

VT + 5V - 4T - 20 = VT 

-4T + 5V = 20 .... ( 2) 

From equation (1) and (2) V = 12 , T = 10

Distance traveled : 12 × 10 = 120 km . 

1. 

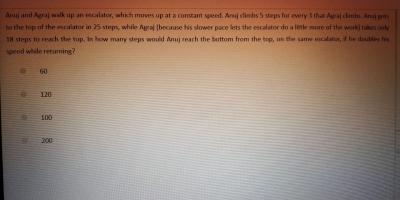
Let the escalator have a total of n steps and let it have moved through m steps by the time Bob took 20 steps.

therefore since Sam runs twice as fast as Bob, the time Sam takes 30 steps is equal to time in which Bob takes 15 steps .

The escalator moved m x 15/20 = 3m/4 steps .

So m + 20 = n and 3m/4 + 30 = n

m/4 = 10

m = 40 steps , n = 60 steps.

If Nick walk half as fast as Bob then let him take t times the time Bob takes => escalator would move through 40t steps and he would take 20t/2 steps

40t + 10t = 60

t = 1.2 times

So Nick would take 12 steps.

Hi Richa, 

The question seems to be incomplete... the speed of the policemen is not known. 

What is the correct answer ?

is it 200?

yes

Answer is 1: 1+√2 ?

Let total distance be 3x and Keshav removes his cloth after x distance

Now we have this equation for remaining journey

Also, let v be Keshav's and a be speed of stream then

2x/(v-a) + 3x/(v+a)= x/a

It means he goes 2x upstream with v-a speed and returns 3x downstream with v+a speed and in the same time clothes travel with the speed of stream i.e a 

Solving this equation 

(2v+2a +3v-3a)*a= (v^2 - a^2)

5va - a^2= v^2 - a^2

5a=v

a/v =5 

Hence required ratio is 5:1 

Sorry for the last line it will be a/v=1/5 

So the ratio will be 1:5

Options ?

10

20

30

60

Let x be time taken by the cyclist while traveling from his home to crossing 

Earlier boy travels 10x distance, in same time train travels vx (assume speed of train be v) 

Now boy travels 10(x+1/2)-6 and train travels vx-6 distance in same time 

Ratio of velocity would be same in both cases so 

10x/vx = {10(x+1/2)-6}/(vx-6)

Solving this we will get v =60 

Alternative approach

The boy is 6km away because he was late for 1/2 hour in which he would have covered 10/2= 5 km so he would have been 1 km away at the same instant when train would have been 6 km away so in same time boy would cover next 1 km and train would cover 6 km to meet at the crossing so ratio of speed of boy to train =1x:6x

1x=10km/h

6x= 60km/h answer

16/3 min 

|____d_____|______________2d___________|

d/2v   + 2d/v = 20 
5d/2v = 20 
d/v = 8. 
|____d_____|______________2d___________|
d/v + 2d/2v = T 
T = 2d/v = 2 x 8 = 16. 

Aniket, 16/3 is not possible 

as 20/(16/3) = 3.xyz

means his average speed is more than thrice while coming back which is not possible

Got it thank you sir

sir, the question is saying twice the length of time but you've taken twice the length of distance 

it's asking for total time in return journey I didn't read it clearly. I got it now

let distance be 'd' and speed of train be x and boy be y 

d/(x+y)=20

d/(x-y)=30

x/d+y/d=1/20

x/d-y/d=1/30

adding both we get 2x/d=1/12

d/x=24  which is the time taken for train to cover distance bw two stations 

hence 24 is the answer

Alternative Approach : 

speed of a train => x 
and the boy's speed => y.

Now when the train goes in the same direction as the boy relative speed is x-y similarly it is x+y for opposite direction.

Now imagine the boy stops moving, relative speed of the train to the boy would just be x right ? 
Hence, x-y, x and x+y  form an AP. ( and distance is constant) time taken should form a HP.

Hence (2 x 20 x 30)/(20+30) = 24 minutes . 

?

Hi Utkarsh,

I can suggest you this

We don't know whose speed is greatest so we have to assume cases 

Let speed be R ,G,S

Case 1 - R>G>S 

R-S= D/2 { let circle be of distance D and we find relative speed of RAM w.r.t to shyam by assuming shyam to be still }

G-S =D/3

subtracting both 

R-G= D/2-D/3= D/6 

so the time t is 6 in this case which is in option

Case 2- G>S>R

S-R =D/2

G-S= D/3

adding both

G-R = 5D/6

t= 6/5= 1.2

So this is also possible hence option 4.8 is the answer 

Note-If you will take other cases either you will get time negative or you will get same values as you got in these cases

Hi rachit

Let total length of circular track is d 

And B is x  away from end of the circular track so C is 2x away from end of the track 

Let's compare ratio of speed of A and C 

In first case A covers d distance and C covers d-2x and in second case A covers 3 lap means 3d distance and C covers 1 whole lap and comes to the position of B in same time so distance traveled is d+ d-x

d/3d= (d-2x)/(d+d-x)

Solving this we get x=d/5 

Let d be 5 so x= 1 

In first lap distanced traveled in same time by A ,B ,C are d , d-x d-2x putting values we get ratio as 5:4:3