23/02/2018 10:48 am
Topic starter
0
Approach please .
79 questions & discussions are there under this sub-topic
3
25/01/2024 12:32 pm
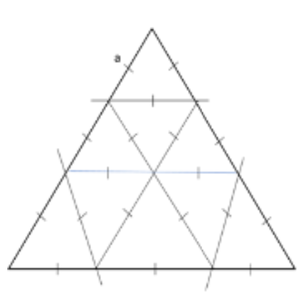
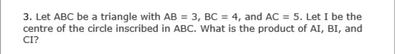Q1. Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is (GEOMETERY TRAINGLES)
A) 5 : 6
B) 3 : 4
C) 2 : 3
D) 4 : 5
This post was modified 8 months ago 2 times by Madhav
Sachin Yadav 27/01/2024 1:10 pm
- Ans- 2:3
Construct an Equilateral triangle and cut of equal lengths from all three sides. So we obtain a hexagon and three equilateral triangles of side 'a' in return.
We know that a hexagon comprises of 6 Equilateral Triangles. Since the side of the hexagon is also 'a', we obtain 6 equilateral triangles in return.
Thus, we have a total of 6 + 3 = 9 equilateral triangles of side 'a'
Ratio of area of Hexagon with Area of Triangle = 6: 9 = 2: 3( Answer).
1
22/02/2018 12:50 pm
0
20/02/2018 5:43 pm
ABC is right angled Traingle. A semicircle with centre O is inscribed inside the triangle shown in the figure. Find area of ABOD.
0
23/02/2018 10:52 am
Hello Kinshuk !
PQR is an Isosceles triangle so PE bisects QR
QE = ER
In ∆PQE => QE² = PQ² - PE² = 7² - PE²
In ∆PDE , DE² = PD² - PE² = 5² - PE²
Now,
QD × DR = (QE + DE) (QE - DE)
=> QD × DR = ( QE)²- ( DE)²
=> QD × DR = 7² -5² = 24
So they can only be 3 × 8 or 4 × 6.
Hence 3+8 = 11,
4+6 =10
Option ( B )
0
06/03/2018 1:04 pm
ABC is a triangle with area 1. AF = AB/3, BE = BC/3 and ED = FD. Find the area of the shaded figure.
Choose one answer.
a. 1/2
b. 13/16
c. 5/9
d. 1/3
Anonymous 06/03/2018 1:16 pm
Hello Abhi,
Please find the solution
A(ABC) = 1
A(ACF) = 1/3 and A(BCF) = 2/3.
A(BFE) = (1/3)*(2/3) = 2/9. So A(AFEC) = 7/9.
A(FBD = A(EBD) = 1/9.
A(EDC) = 2*A(EBD) = 2/9.
A(FDA) = (1/2)*A(FBD) = 1/18.
A(ADC) = A(AFEC) - A(EDC) - A(FDA) = (7/9) - (2/9) - (1/18) = 1/2
0
14/03/2018 6:33 pm
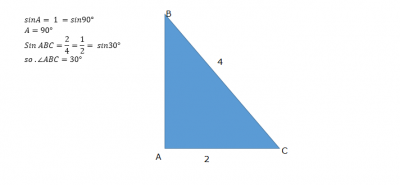
In triangle ABC, BC = 4 units, AC = 2 units and sin A = 1. What is angle ABC?
- 30
- 60
- 45
- 90
0
23/03/2018 4:35 pm
Topic starter
Hello sir,
Please solve
0
24/03/2018 1:38 pm
32 – (1+x)2 = 33-(2-x)2
1+x2+2x=4+x2-4x
6x = 3
x =1/2
AE = 3(sqrt3)/2
AD2 =(3(sqrt3)/2)2 + (1/2)2 =27/4 + 1/4 = 7
AD = sqrt7
0
26/03/2018 11:35 am
Hello sir,
please solve this question
0
31/03/2018 2:34 pm
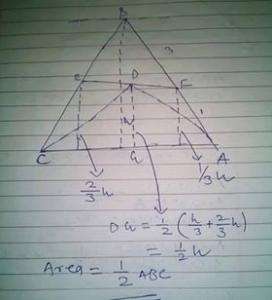
In triangle ABC ,Produce a line from B to meet AC,meeting at D and From C to AB,meeting at E.let BD and CE meeet at X.let triangle BXE have area a,triangle BXC have area b and triangle CXD have area c.find the area of quadrilateral AEXD in terms of a,b,and c
a) bc(2a+b+c)/b^2-ac
b)ac(a+2b +c)/b^2-ac
c)abc/b^2-ac
d)ab(a+b +2c)/b^2-ac
0
31/03/2018 2:34 pm
ake a special case. Assume ABC is an equilateral triangle.
Let's assume D is the mid point on AC and E is the mid point on AB.
Now Area(BXE) = Area(CXD) = a = c
Then for this case Area(BXC) = b = 2a
And area of AEXD = 2a (it's very simple to calculate now)
Now, check all options:
- a) 2a*a(2a+2a+a)/4a^2-a^2 = 10a/3
- b) a*a(6a)/4a^2-a^2 = 2a
c)a*2a*a/4a^2-a^2 = 2a/3
- d) a*a(a+2a+2a)/4a^2-a^2 = 5a/3
Only b) matches. So, it is the answer.
Hemant 23/06/2018 9:51 pm
Three altitudes of a triangle are 12cm, 20cm and 25 cm. Find the perimeter of the triangle. How to solve this one?
TG Team 24/06/2018 7:23 pm
Hello Hemant!
Ratio of sides :
1/12 : 1/20 : 1/15 => 5x : 3x : 4x
Area => 1/2 • 3x•4x = 1/2 • 12 • 5x
x = 5
Perimeter => 5x + 4x + 3x = 5 × ( 5+3+4) = 60 🙂
0
23/05/2018 1:58 am
The perimeter of a right triangle is 12+8√3. The sum of the squares of the three sides is 294. Find the length of the hypotenuse.
0
23/05/2018 7:31 pm
Given that P2+ B2 + H2 = 294
and P2 + B2 = H2
So, H2 + H2 = 294
2H2 = 294
H2 = 147 = 49 x 3
H = 7 sqrt(3)
Page 1 / 6
Next