24/08/2018 7:40 am
0
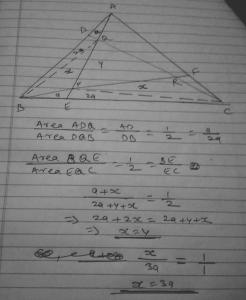
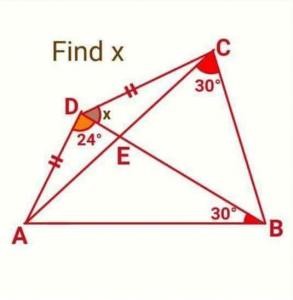
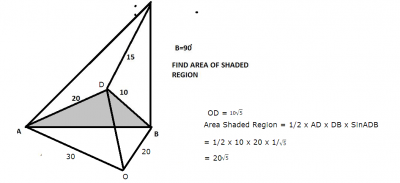
The perimeter of an isoceles right triangle is 2k , what is its area ?
Let the area of a triangle T be numerically equal to its perimeter. Find the radius of the inscribed circle .
TG Team 24/08/2018 2:44 pm
We know ,
Area of a triangle = Semiperimeter × inradius of the triangle
So , T = ( a + b + c)/2 × r
According to the question
(a + b + c) = ( a + b + c)/2 × r
r = 2 units.
0
29/08/2018 3:05 pm
0
31/08/2018 11:40 pm
ABC is a right angled triangle , right angled at B. The bisector of the external angle at A meets CB produced at D. If AC = 5 cm , BC = 4 cm , find the length of CD.
TG.Raman 01/09/2018 5:53 pm
AB/AC = BD/DC [ External Angle Bisector Theorem ]
3/5 = BD/( BD + 4)
BD = 6
Hence CD = 6 +4 = 10 cm.
0
03/09/2018 2:31 pm
0
23/09/2018 5:06 pm
0
01/10/2018 2:41 pm
- Data sufficiency question
is ∆ABC an equilateral triangle?
I.the orthocentre lies outside ∆ABC
II.The circumcentre coincides with the orthocentre
TG Team 01/10/2018 6:08 pm
The orthocentre of a triangle is the intersection of the triangle's three altitudes.
In an acute angled triangle orthocentre is inside the triangle .
In a right triangle it is on the vertex at the right angle.
In an obtused angle triangle orthocentre will always lie outside the triangle.
So using (i) we can say triangle is obtused angle triangle ( not an equilateral ) Hence (1) is sufficient.
A triangle in which any two of circumcentre , orthocentre and centroid coincide is equilateral triangle so the 2nd statement is also sufficient .
Hence , each statement is independently sufficient.
0
02/10/2018 4:12 pm
TG Team 02/10/2018 6:13 pm
B is multiplied by 25, LCM (A,B) remains unchanged so A has 53 in its prime factorization .
When A is multiplied by 8 ,LCM (A,B) remains unchanged so B has 24 in its prime factorization .
And A can have 20 or 21 => 2 cases
for each case exponent of 7 can range from 0 to 4 in A so 5 cases
Total : 2 x 5 = 10 cases
0
12/10/2018 9:23 pm
TG Team 13/10/2018 12:32 am
Draw a line parallel to BF from D .
AF : FC = 3 : 7
AF : AC = 3 : 10
AC = 40 cm
0
12/10/2018 9:36 pm
0
12/10/2018 9:40 pm
Utkarsh Garg 12/10/2018 10:27 pm
This post was modified 6 years ago by Utkarsh Garg
Area of equi triangle= √3/4* a^2 --1
Also 1/2* a * (4+3+5)= 6a --2
from 1 and 2
6a= √3/4* a^2
a=8√3
therefore area=√3/4* a^2= 48√3
0
15/10/2018 9:27 pm
0
15/10/2018 10:05 pm
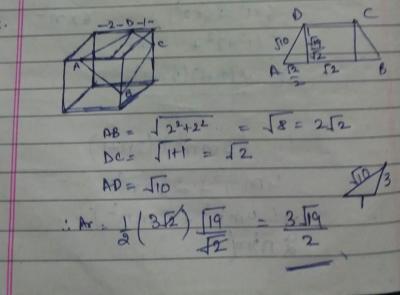
A, B, C, D are four points on the edges of a 3 ´ 3 ´ 3 cube which are at a distance of 1 unit from the closest vertex as shown in the figure. If a plane is passed through the points A, B, C and D, what will be the area of the cross-section formed?
Sir how do we find the height of the cross sectional isosceles trapezium in this ?
0
17/10/2018 12:51 am
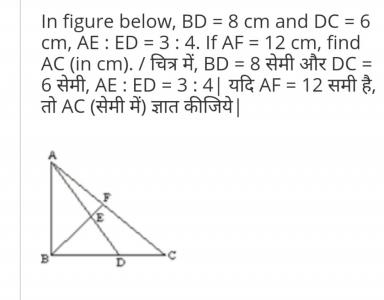
The diagram shows 78 points each at equal distance of 1 unit from its nearest points. AB and CD intersect at E. Find the area of the triangle ACE approximately in square units.
