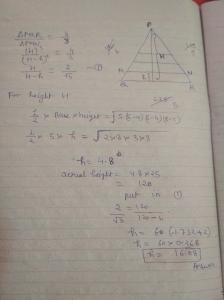30/10/2018 6:15 pm
0
in circle O , chords CD and AB intersect at right angles at E. if CE=8 and DE=6, AE = 24 What is the radius of circle.
0
30/10/2018 6:19 pm
in a triangle ABC, AB=10, BC=14 and AC=18. and D lies on AC with BD=10. What is the ratio of AD:CD.
a)14:10
b)18:14
c)22:11
d)38:16
0
30/10/2018 6:27 pm
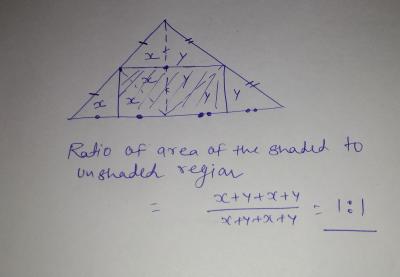
Two circles each with radius 1 are inscribed so that their centers lie along the diagonal of square. Each circle is tangent to two sides of the square and they are tangent to each other. Find the area between the circles and the square.
a) 6+4sqrt2-2pie
b)10-2pie
c)4+2sqrt2 -2pie
d)8sqrt2-2 pie
0
05/11/2018 12:35 pm
In a right angle triangle AC = 1, Angle B = 90° and Angle A = 15° Find the area of the triangle ABC.
1/4 square units
1/8 square units
0
09/11/2018 9:45 pm
What's the length of largest equilateral triangle that can be inscribed in an equilateral triangle of side length 1?
0
09/11/2018 9:48 pm
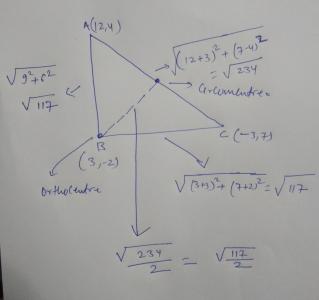
(3,-2), (12,4) and (-3,7) are the three vertices of a triangle. Then the distance between the orthocenter and circumcenter of this triangle is-
aniket prajapati 10/11/2018 1:08 pm
Sides are √117 √117 √234 which is a isosceles right angle triangle in which mid point of hypotenuse is orthocentre and point where right angle is formed is orthocentre so the distance becomes half of hypotenuse which is (1/2)*√234 gives √117/2
0
09/11/2018 10:58 pm
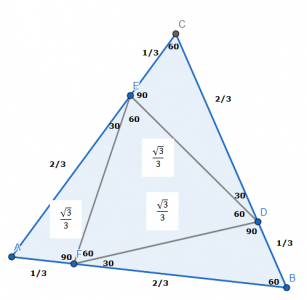
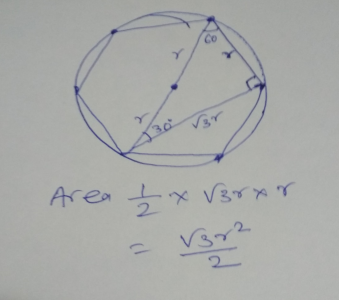
In a circle of radius r units, six points equally spaced are placed on the circumference. ΔABC is formed by joining three points such that ΔABC is neither isosceles nor equilateral. What is the area of ΔABC?
0
22/11/2018 2:52 pm
Q44,Q45
aniket prajapati 23/11/2018 11:47 am
45.
If perimeter is given max area will be of equilateral traingle
A= √3/4*(44/3)
Hence none of these
0
02/12/2018 11:35 am
0
11/12/2018 2:32 pm
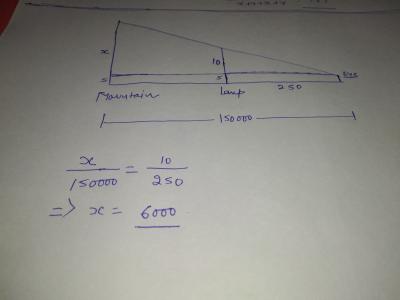
- A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the
lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angle
of 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The
height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
Options:
1) 300 feet
2) 600/√3 feet
3) 300√3 feet
4) 600 feet
5) None of the above
TG.Raman 11/12/2018 4:40 pm
Boat stationed at C forms a 30-60 - 90 triangle (COA), Hence ratio of sides :
AO : OC : AC = 1 : sqrt3 : 2
OC = 300 sqrt 3
Similarly boat stationed at East of the lighthouse forms a 45 - 45 - 90 triangle.
Ratio of the sides 1 :1 : sqrt 2
OB = 300
OA = Height of the light house
C : Boat stationed at North
B : Boat stationed at East
Shortest distance between boats : BC
BC^2 = OC^2 + OB^2
BC^2 = 300^2 +(300sqrt3)^2
BC = 600.
0
19/12/2018 9:20 pm
