30/04/2019 12:01 am
0
Gaurav Jain 30/04/2019 11:08 am
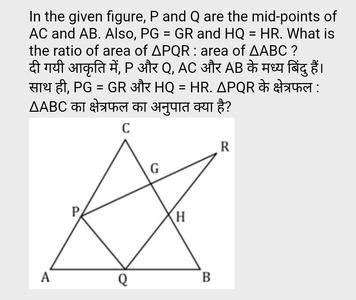
P and Q are mid points, hecne PQ=1/2BC
Now are of ABC is = 1/2 BC* h (considering BC as base)
now distance of A from PQ will be 1/2 h (using similarity)
same way distance of G from PQ will 1/2 h (because GH and PQ are parallel lines)
Hence distance of R from PQ will be 'h'.
So both the triangles ABC and PQR have same height, but base of PQR is 1/2 the base of ABC
Hence ratio of ares is 1/2
0
02/09/2019 9:30 am
Hotel trinity grand has a triangular terrace with sides 20m, 34m and 42m. A square shaped swimming pool is to be constructed such that one of its sides coincides with the largest side of the terrace and two vertices of the swimming pool touch other two sides of the terrace.
Q1. what is the perimeter of the pool?
Q2. What is the sum of the perimeters of the three triangular regions which are not covered by the pool?
Q3. what is the area of the terrace?
Gaurav Jain 05/09/2019 4:43 pm
find lenght of height on biggest side using area
then use similarity to calculate the length of square
0
02/09/2019 9:37 am
There is a country called Tolagola in the shape of a parallelogram ABCD. M,N,O and P are the mid points of DC, DA, AB, and BC respectively. The government decided to divide the country into 9 states by drawing 4 straight lines DP, NB, AM and OC. OC meets with NB and DP at S and T respectively. Also, AM meets with NB and DP at R and Q respectively.
Q1. If the area of AOSR is 240 kmsq, what is the area of CTP?
Q2. What is the area QTSR if area ABCD is 1000 kmsq.?
Q3. If the area DTC is 1600 km sq, what is the area NSTD?
Q4. What is the ratio of the areas PTSB and ARN?
0
21/04/2024 3:42 pm
0
17/05/2024 3:09 pm
As shown in the figure ∆ABC is a right angled triangle and D is a point on AC such that ∠BDA = 120°. If BD = DC = 6 units, then what is the in-radius of ∆BDC?
A. 2 B. √3 C. 2√3 D. 1
Page 6 / 6
Prev