02/06/2018 12:43 pm
0
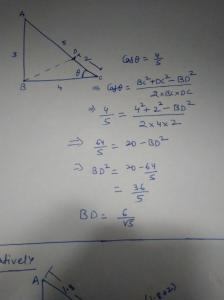
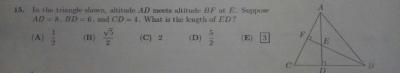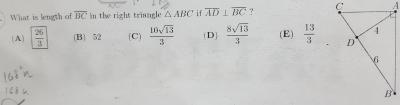The sides of a right triangle are 3 4 5
A point is taken on the hypotenuse at a distance of 2 cm from the vertex adjacent to the 4 side. Find the distance from this point to the vertex of the right triangle.
TG Team 01/07/2018 2:07 pm
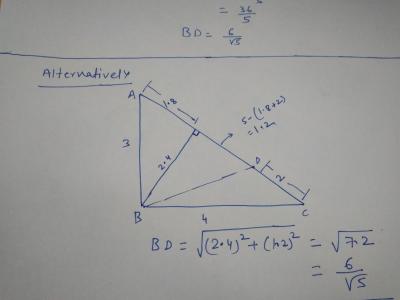
The alternate approach for the question
The sides of a right triangle are 3 4 5
A point is taken on the hypotenuse at a distance of 2 cm from the vertex adjacent to the 4 side. Find the distance from this point to the vertex of the right triangle.
0
02/06/2018 5:35 pm
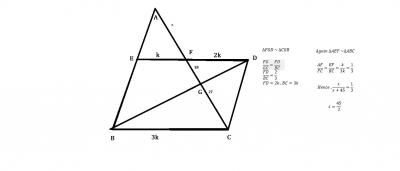
Let's say MN intersect AX at O ,
MO = 1/2 BX
∆AMO and ∆ABX are similar triangles so
Area∆ AMO/ Area∆ABX = MO²/BX² = 1/4
So if Area of ∆AMO = x ,then Area ABX = 4x and Area MOXB = 4x - x = 3x ( shaded area )
Area of ∆ABC = 2 × Area ∆ABX = 8x
Hence required ratio = 3x/ 8x = 3 : 8
0
09/07/2018 1:01 pm
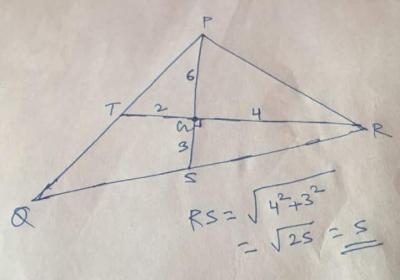
two medians PS and RT of ∆PQR intersect at G at right angles. If PS=9 cm and RT =6cm then the length of RT is
a) 10
b)6
c)5
d)3
TG Team 09/07/2018 2:41 pm
Hi Nancy
Please see if the question is complete.
I thing there is a typographical error , the length of RT ( 6cm ) is already mentioned in the question .
Nancyjain 09/07/2018 3:33 pm
Two medians PS and RT of ∆PQR intersect at G at right angles. If PS =9CM and RT =6 cm,then length of RS is
a) 10
B) 6
C)5
D)3
TG Team 09/07/2018 4:09 pm
Centroid divides the medians in 2 : 1 .
So PG : GS = 2 : 1
GS = 3 cm , PG = 6 cm
Again RG : GT = 2 : 1
GT = 2cm , RG = 4 cm
∆GSR is a right angled ∆ .
So , RS² = RG² + GS²
RS ² = 3² + 4²
RS = √25 = 5 .
0
09/07/2018 9:52 pm
ABCD is a parallelogram, AC and BD are diagonals intersecting at O. X and Y are centroids of ∆ADC and ∆ABC respectively. If BY=6 then OX=?
A)2
B)3
C)4
D)6
TG Team 10/07/2018 12:52 am
Since centroid divides the median in 2 : 1 ,
BO : OY = 2 : 1
OY = 6/2 = 3.
OY = OX = 3.
Option (B)
0
25/07/2018 9:59 pm
Hi Sir, can you help me with this question? P.S- I was not able to post it in "Circles" section, so posting it here.
TG Team 25/07/2018 10:38 pm
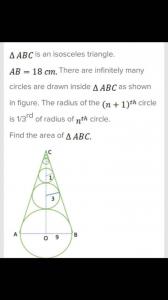
Hello Richa ,
Here , OC = Altitude on AB = Sum of diameters of the circles + radius of the largest circle
OC = 9 + 6 + 2 + 2/3 +..... = 9 + ( 6)/ ( 1-1/3) = 18
Area of the Triangle ABC = 1/2 x OC x AB
1/2 x 18 x 18 = 162 sq units .
0
25/07/2018 10:14 pm
A right triangle with integer side lengths a, b and c satisfies a<b<c and a+c=81. what is the maximum area of the triangle given these conditions?
(A) 480 unit sq
(B) 504
(C)580
(D) 630
0
30/07/2018 3:13 pm
Sir please solve this question
0
01/08/2018 1:53 pm
Hey Sir, please help with this problem:
TG Team 01/08/2018 2:15 pm
Hello Richa ,
In triangles ADC and BDE
Angle A = Angle B
Angle D = Angle D (Each 90)
Hence , triangle ADC similar triangle BDE
AD/CD = BD/ED
8/4 = 6/ ED
ED = 3 units .
0
07/08/2018 4:01 pm
find value of x ?
0
07/08/2018 4:33 pm
find x if given quadrilateral is parllelogram
0
08/08/2018 5:50 am
Hey Sir, posting a question below. Please help with the solution.
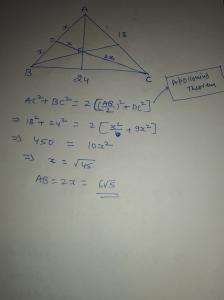
In a triangle ABC, BC =24, AC=18 and the medians to side BC and AC are perpendicular. Find AB.
0
08/08/2018 1:05 pm
Sir please explain this solution
TG Team 08/08/2018 3:39 pm
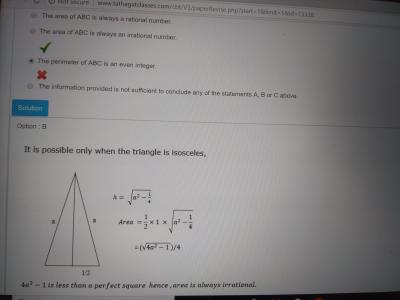
Sides: a, a and 1
Two cases:
(i) a is an even integer , sum of two even integer and 1 is always odd
(ii) a is an odd integer ,
odd integer + odd integer + 1 = an odd integer
so Option C is false .
Using Pythagoras Theorem : Altitude of the triangle = sqrt {a^2 - (1/2)^2} =
Area = 1/2 x Base x Altitude
=> sqrt{4a^2 -1}/4
4a^2 is a perfect square, so sqrt{4a^2 -1} is irrational
So area is always an irrational Number .
0
19/08/2018 7:27 am
TG Team 19/08/2018 11:47 am
Triangle CAD ~ Triangle ABD
CD/AD = AD/BD
AD² = CD × BD
16 = CD × 6
CD = 16/6
BC = 8/3 + 6 = 26/3
Option (A)
0
19/08/2018 3:34 pm
cos (2pi/7) + cos (4pi/7) + cos (6pi/7) = ?
options are 1, 1/2, -1/2, -1,
